精排 – 多目标模型

简单的多目标模型

模型结构

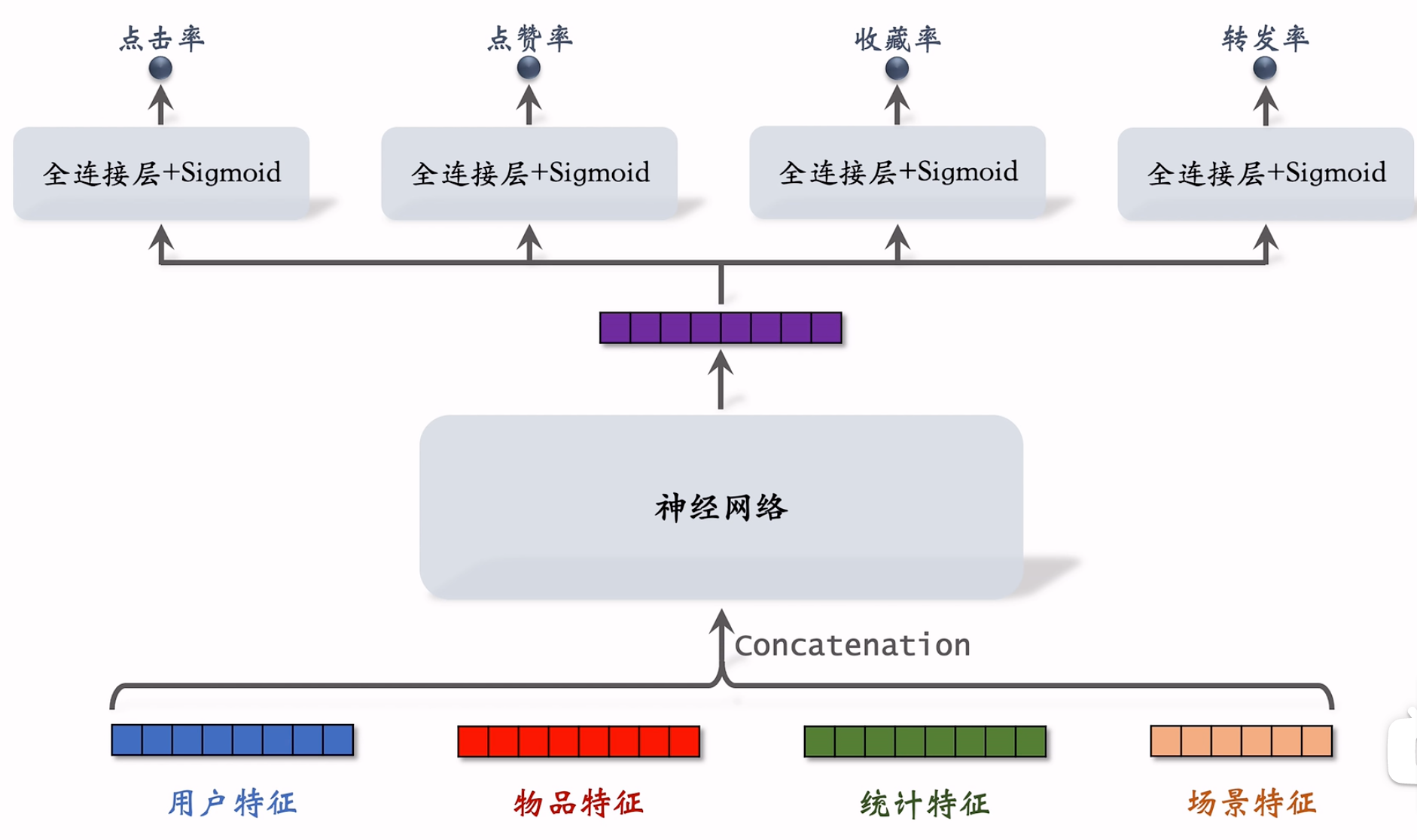
损失函数和训练

问题

数据集通常是类别及不平衡的，比如总共1000次曝光，其中只有100次点击，10次收藏，收藏次数对于曝光来说相差极大。

解决方案：通常使用负样本降采样的方法。

预估校准：负样本降采样之后，就改变了各个目标的实际分布，所以模型的预估值是有偏的，需要进行校准，通常使用Facebook提出的公式校准法。
$$
p_{true} = \frac{\alpha · p_{pred}}{(1-p_{pred})+\alpha · p_{pred}} \tag{1}
$$

MMoE

模型结构

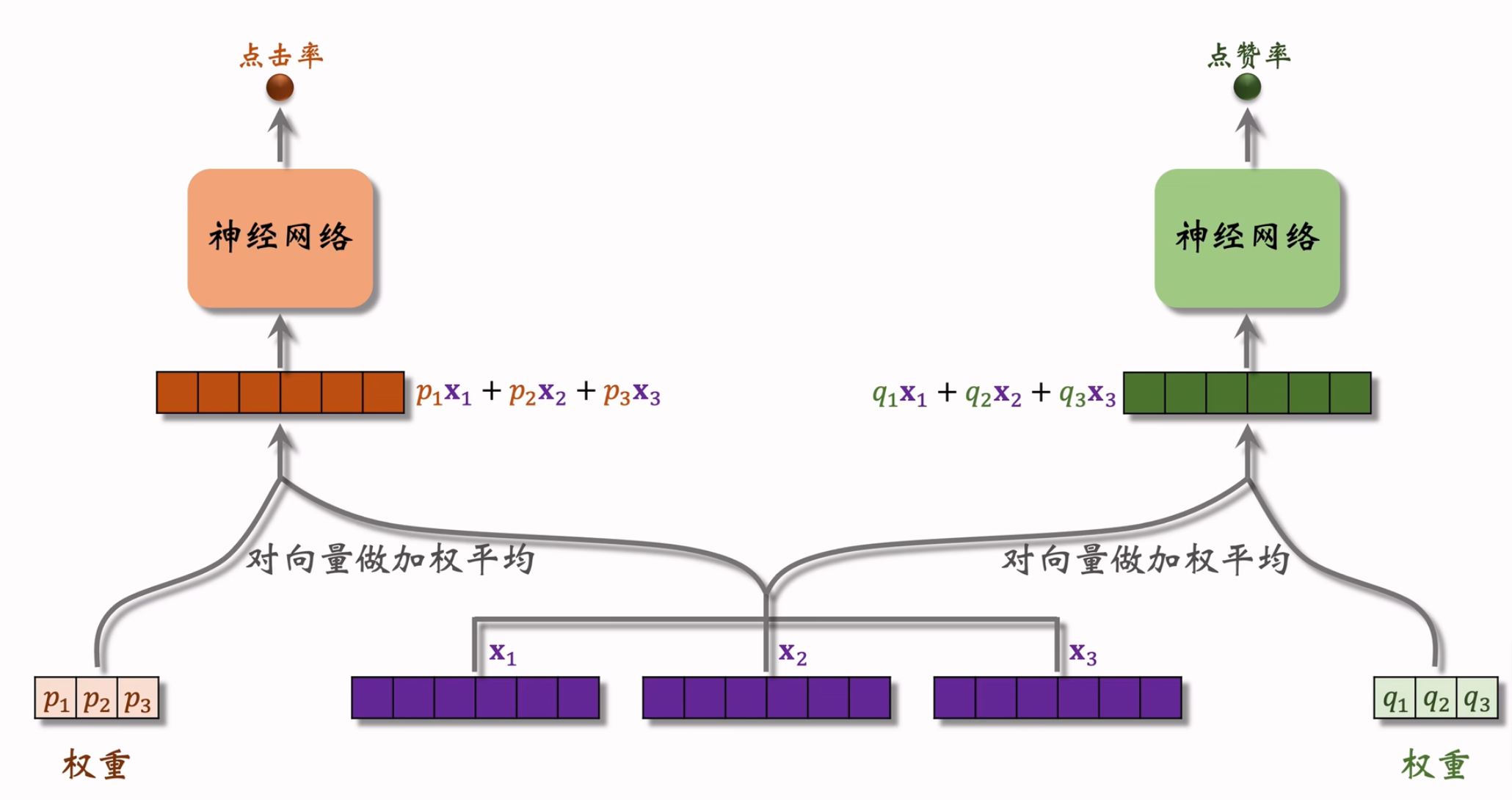
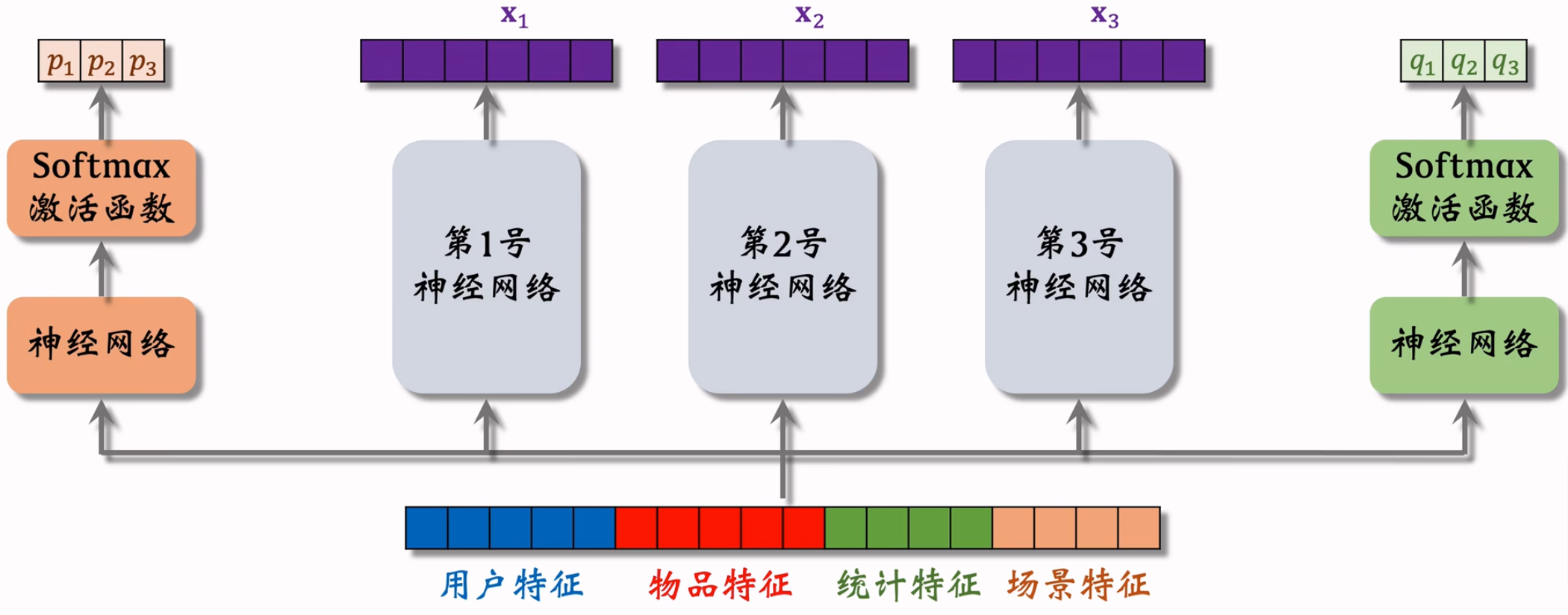
极化现象

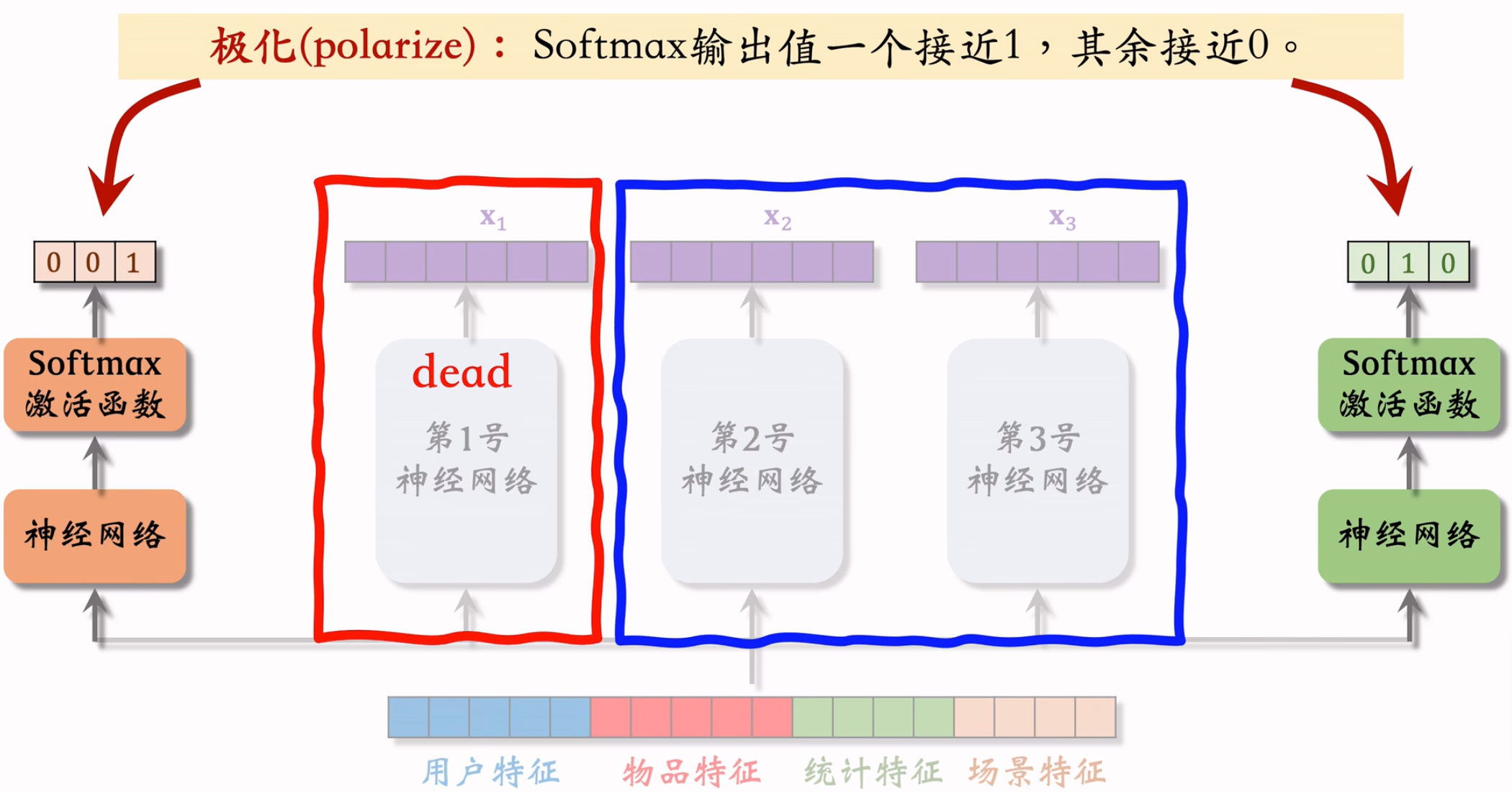
解决方案是对softmax的输出使用dropout。比如softmax的n个输出被mask的概率都为10%，也就是每个专家有10%的概率不参与本次预测。

假如训练过程中发生了极化现象且对应专家被mask了，则最终预测输出为0，效果奇差，所以dropout可以解决极化现象，参考文献《Recommending What Video to Watch Next: A Multitask Ranking System》。

多目标预估分数融合

简单加权和

$$
p_{click} + w_1·p_{like} + w_2·p_{collect} + …
$$

点击率乘以其他项加权和

$$
p_{click} · ( 1 + w_1·p_{like} + w_2·p_{collect} + … )
$$

某短视频APP1的融分公式

$$
(1 + w_1 · p_{time})^{\alpha_1} · (1 + w_2 · p_{like})^{\alpha_2} …
$$

某短视频APP2的融分公式

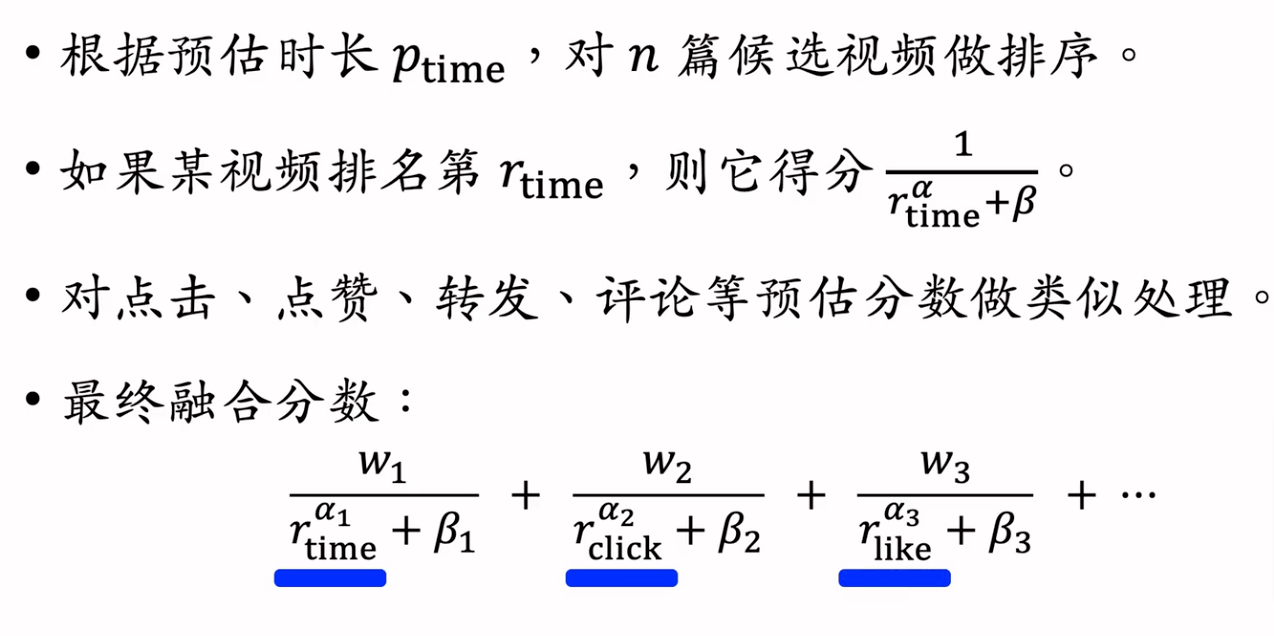
某电商的融分公式

$$
p_{click}^{\alpha_1} · p_{cart}^{\alpha_2} · p_{pay}^{\alpha_3} · p_{price}^{\alpha_4}
$$

粗排 – 三塔

模型结构

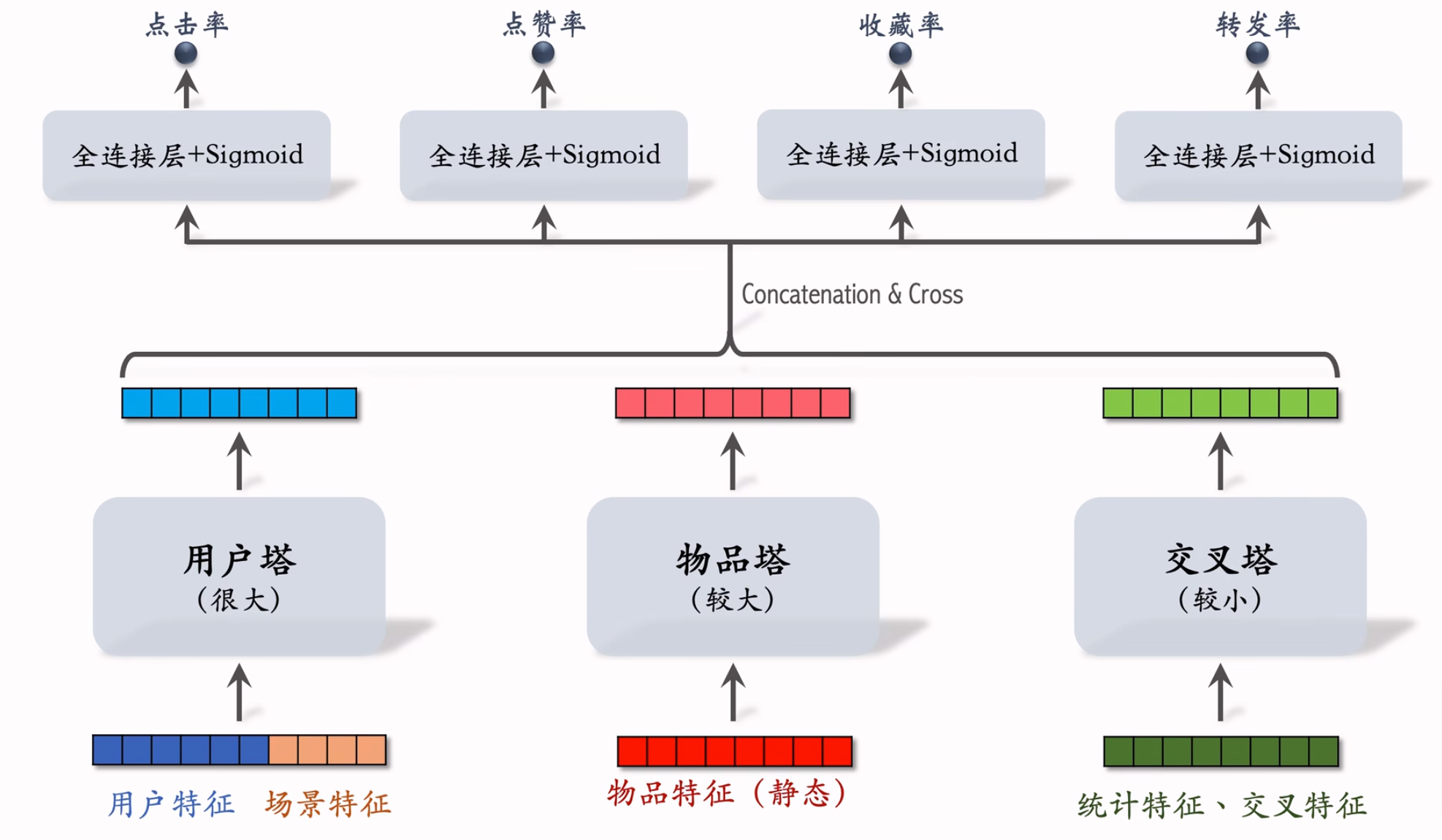
• 用户塔：因为每次推理只有一个用户，只做一次推理，所以总计算量不大，所以可以设计的很复杂。
• 物品塔：每次推理会有n个候选物品，因为物品特征比较稳定，所以可以通过缓存的方式避免大多数推理。只需要把没命中缓存的物品推理即可，因此总计算量也不算大，所以可以设计的比较复杂。
• 交叉塔：统计和交叉等特征更新频繁，所以不能缓存。又因为每次推理n个候选物品就需要推理n次，所以通常设计的比较简单。

参考文献

公开课地址：GitHub

推荐系统中的多任务学习与多目标排序工程实践（上）：https://zhuanlan.zhihu.com/p/422925553

本文永久更新地址: https://notlate.cn/p/006d8316b498cd6e/