ItemCF召回
ItemCF原理
$$
\sum_{j} like(user, \, item_j) · sim(item_j, \, item_{候选物品}) \tag{1}
$$
用图表示为:
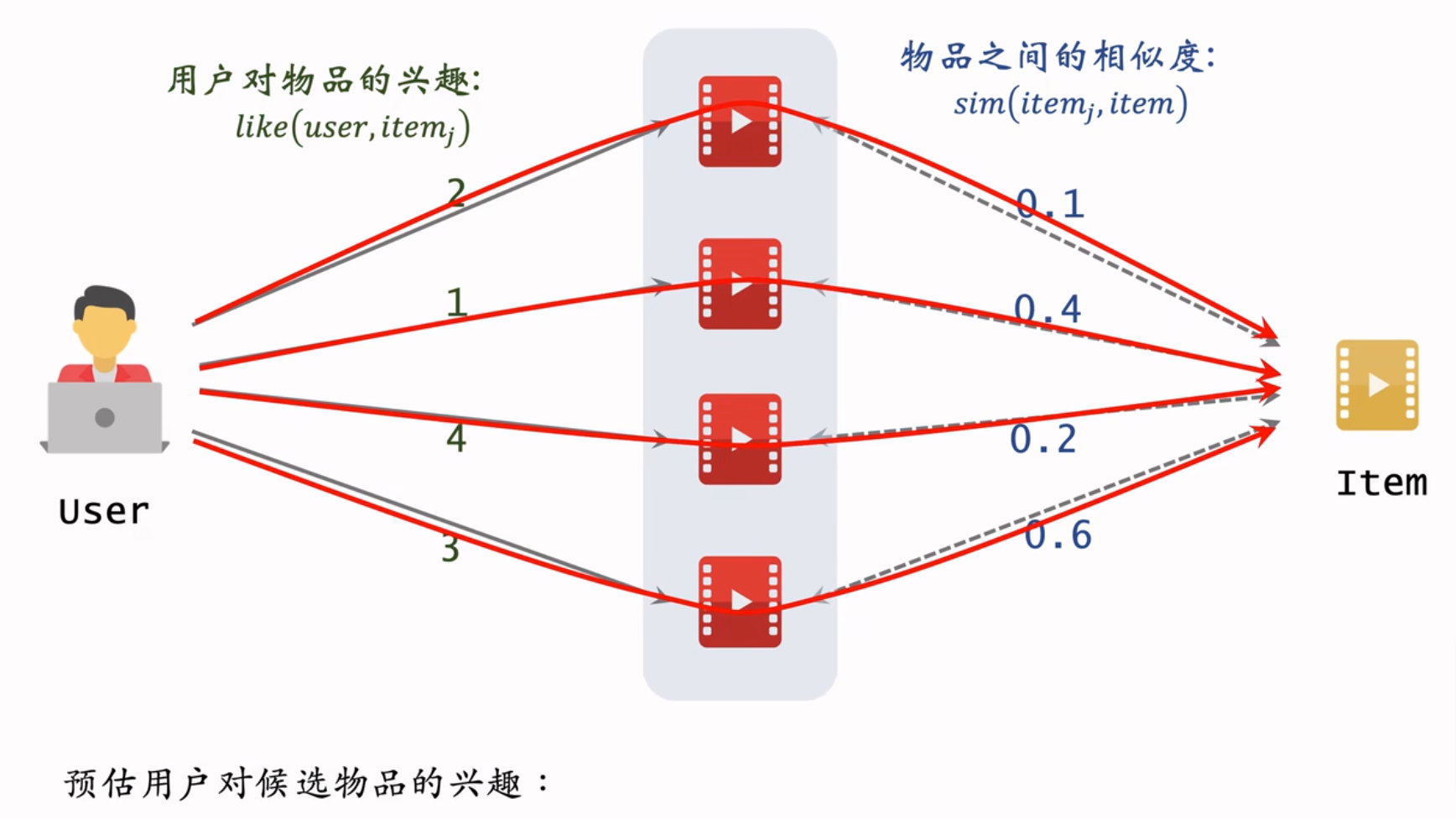
物品相似度计算方法
$$
sim(i_1, i_2) = \frac{|V|}{\sqrt{|W_1| · |W_2|}} \tag{2.1}
$$
其中$i_1$和$i_2$是两个物品,$W_1$是喜欢物品$i_1$的用户集合,$W_2$是喜欢物品$i_2$的用户集合,$V$是同时喜欢两个物品的用户集合$V = W_1 \cap W_2$,$|·|$表示集合的元素总数。
此公式只考虑了用户对物品的喜欢,但是没有考虑对物品的喜欢程度。改写如下:
$$
sim(i_1, i_2) = \frac{\sum_{v \in V} like(v, i_1) · like(v, i_2)}{\sqrt{\sum_{u_1 \in W_1} like(u_1, i_1)^2} · \sqrt{\sum_{u_2 \in W_2} like(u_2, i_2)^2}} \tag{2.2}
$$
上式中分子是同时喜欢两个物品的用户对两个物品的喜欢程度乘积再累加;分母是两个用户分别对两个物品的喜欢程度的平方根号再相乘。这个就是余弦相似度的公式,两个物品向量表示如下:
$$
i_1 = \Big( like(u_{11}, i_1), like(u_{12}, i_1), … , like(u_{1n_1}, i_1) \Big) \tag{3.1}
$$
$$
i_2 = \Big( like(u_{21}, i_2), like(u_{22}, i_2), … , like(u_{2n_2}, i_2) \Big) \tag{3.2}
$$
ItemCF召回总体流程
离线流程:
- 建立“用户->物品”的索引,记录每个用户最近交互过的物品ID,可以计算出用户对每个物品的喜欢程度。给定任意用户ID可以找到他近期感兴趣的物品列表。
- 建立“物品->物品”的索引,用公式$(2.1)$计算两个物品相似度,每个物品索引最相似的K个物品。给定任务物品ID可以找到这K个物品。
在线流程:
- 给定用户ID,通过“用户->物品”索引,找到用户近期感兴趣的N个物品(lastN)。
- 遍历lastN物品列表,从“物品->物品”索引中找到每个物品最相似的K个物品。
- 以上两步最多可获取到$NK$个物品,用公式$(1)$预估用户对每个物品的兴趣分数。
- 分数从高到低降序排列,返回前S(比如100)个物品。
ItemCF总结
特点:用户物品索引和物品物品索引,离线计算量大,在线计算量很小。
缺点:相似度大小是计算喜欢这两个物品的用户交集的大小。如果这个交集中的用户同属于一个小圈子,则相似度就不准确(类似于下图),解决方案则是引入用户重合度,即Swing召回通道。
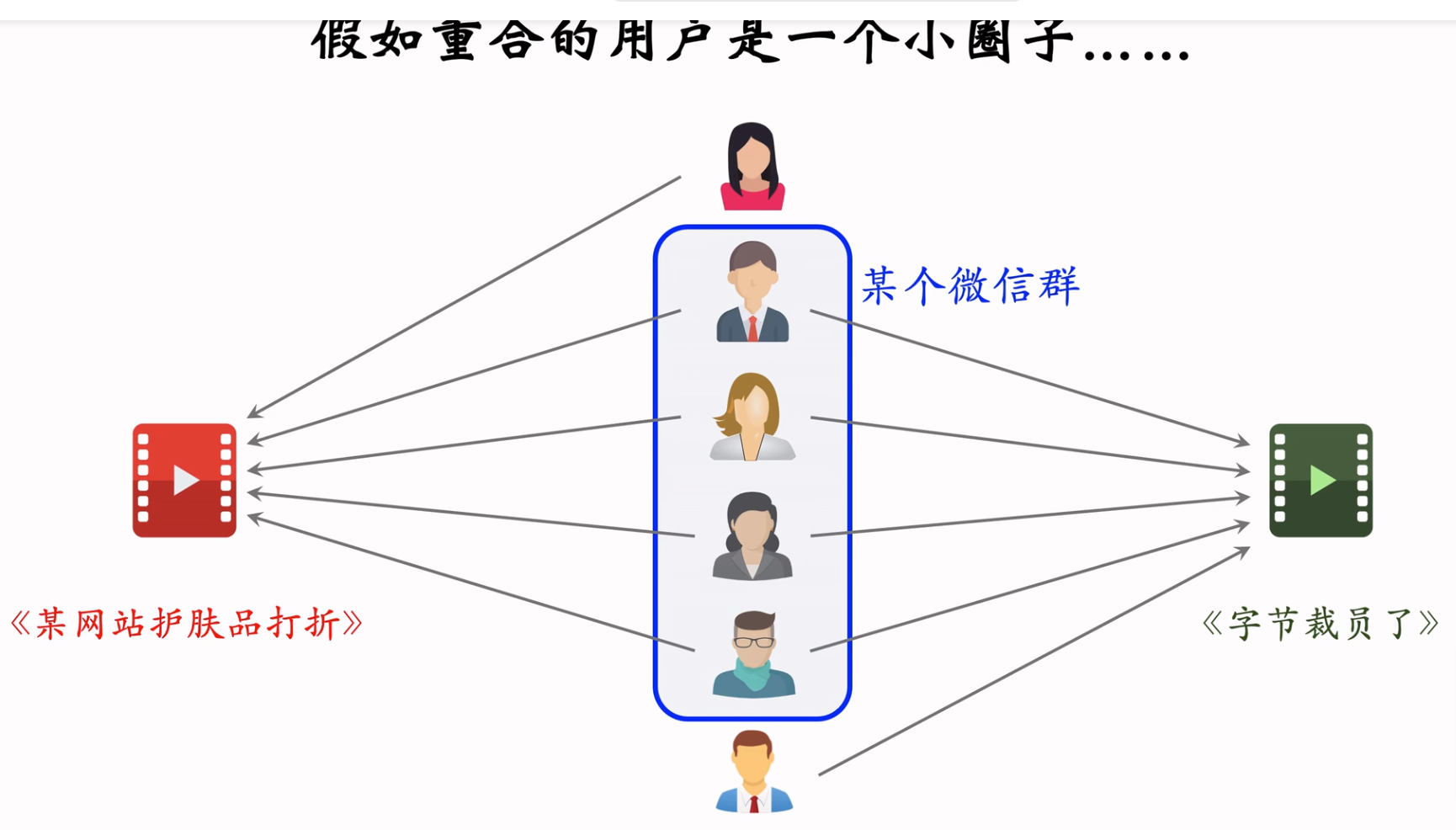
Swing召回
用户重合度计算方法
记用户$u_1$喜欢的物品集合是$J_1$,用户$u_2$喜欢的物品集合是$J_2$,则用户重合度定义为两个用户喜欢相同物品数:
$$
overlap(u_1, u_2) = |J_1 \cap J_2| \tag{4}
$$
则公式$(2.1)$可以改写为:
$$
sim(i_1, i_2) = \sum_{u_1 \in V} \sum_{u_2 \in V} \frac{1}{\alpha + overlap(u_1, u_2)} \tag{2.3}
$$
显然,如果两个用户的重合度比较高,则其对物品相似度的贡献较小。
其他逻辑与ItemCF相同
UserCF召回
UserCF原理
$$
\sum_{j} sim(user, user_j) · like(user_j, item) \tag{5}
$$
用图表示则如下:
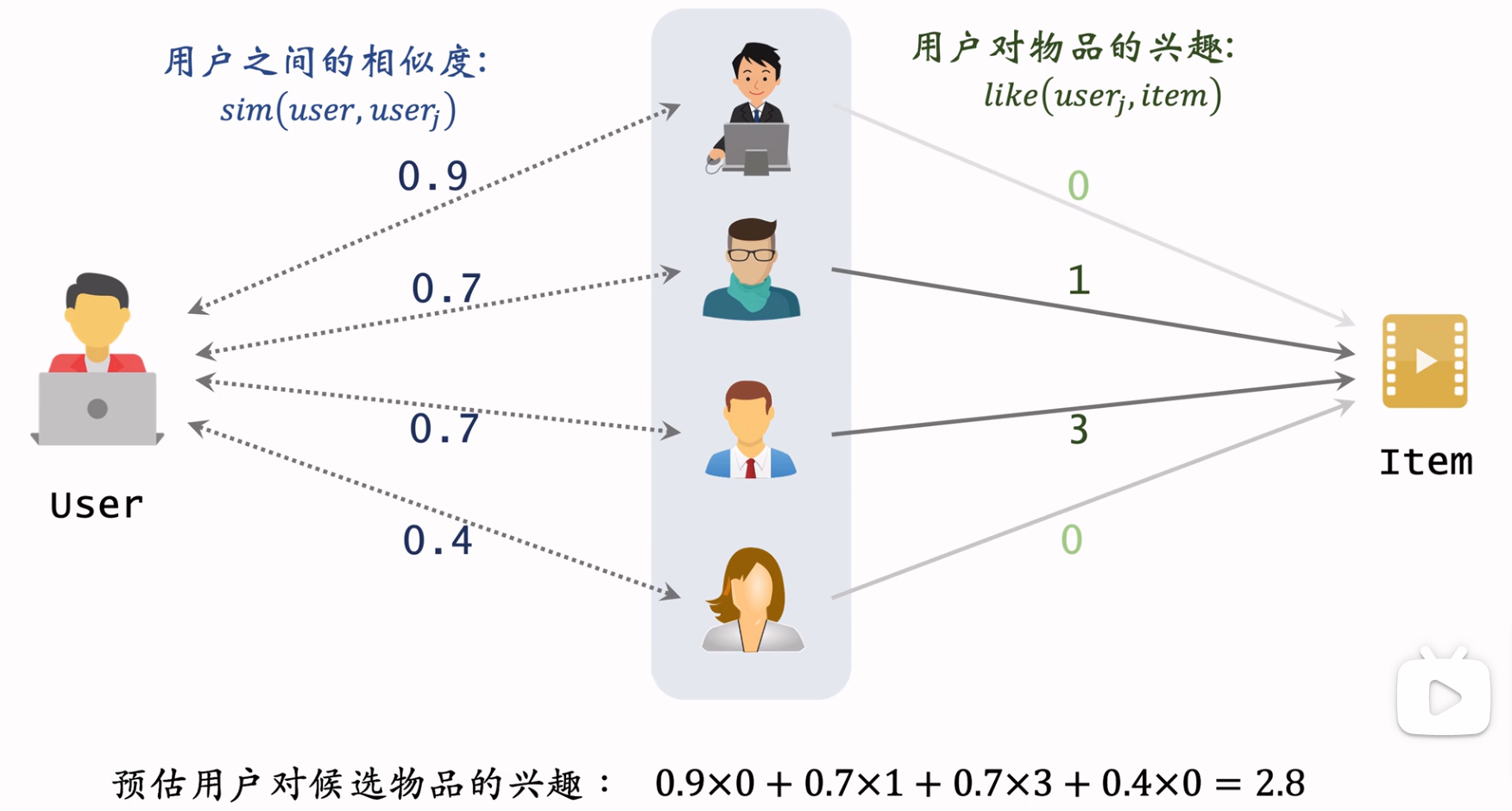
用户相似度计算方法
记用户$u_1$喜欢的物品集合为$J_1$,用户$u_2$喜欢的物品集合为$J_2$。类似于用户重合度,定义用户相似度为同时喜欢的物品个数占比。公式如下:
$$
sim(u_1, u_2) = \frac{|J_1 \cap J_2|}{\sqrt{|J_1|·|{J_2}|}} \tag{6.1}
$$
上述公式的分子为两个用户同时喜欢的物品个数,则热门物品相对于冷门物品的权重来说就要高很多,也就是需要降低热门物品的权重。如果把公式$(6.1)$中每个物品的权重看作是1,也就是可以改写成:
$$
sim(u_1, u_2) = \frac{ \sum_{l \in |J_1 \cap J_2|} 1}{\sqrt{|J_1|·|{J_2}|}} \tag{6.2}
$$
把上式中的分子中的权重根据物品热门程度$n_l$(即喜欢物品$l$的用户数)可以改写成:
$$
sim(u_1, u_2) = \frac{ \sum_{l \in |J_1 \cap J_2|} \frac{1}{1 + n_l}}{\sqrt{|J_1|·|{J_2}|}} \tag{6.3}
$$
显然,如果物品热门程度比较高,则其对用户相似度的贡献越小。
UserCF召回总体流程
离线流程:
- 建立“用户->物品”的索引,记录用户最近交互过的物品ID,并计算好用户对每个物品的喜欢程度(可自定义,例如不同交互行为分值不同,所有交互行为分值累加和表示喜欢程度)。给定任意用户ID,可以找到他近期最感兴趣的物品列表。
- 建立“用户->用户”的索引,用公式$(6.3)$计算用户相似度,并索引与之最相似的K个用户。给定用户ID,可以找到这K个用户。
在线流程:
- 给定用户ID,通过“用户->用户”的索引,找到最相似的K个用户。
- 遍历K个用户列表,通过“用户->物品”的索引,找到每个用户近期最喜欢的N个物品列表(lastN)。
- 这样最多取回$NK$个相似物品,然后用公式$(5)$预估该用户对每个物品的兴趣分数
- 按照分数从大到小降序排列,取分数最高的S(比如100)个物品返回。
向量召回
离散特征编码
编码方式
机器学习中,通常把离散特征编码为数字。以性别特征为例,其取值只有3种(男,女,未知),编码方式有:
- 序号编码:即对特征取值按照一定顺序编号,例如:男->0,女->1,未知->2
- One-Hot编码:总共3个取值,则编码结果维度是3,例如:男->[1, 0, 0],女->[0,1,0],未知->[0,0,1]
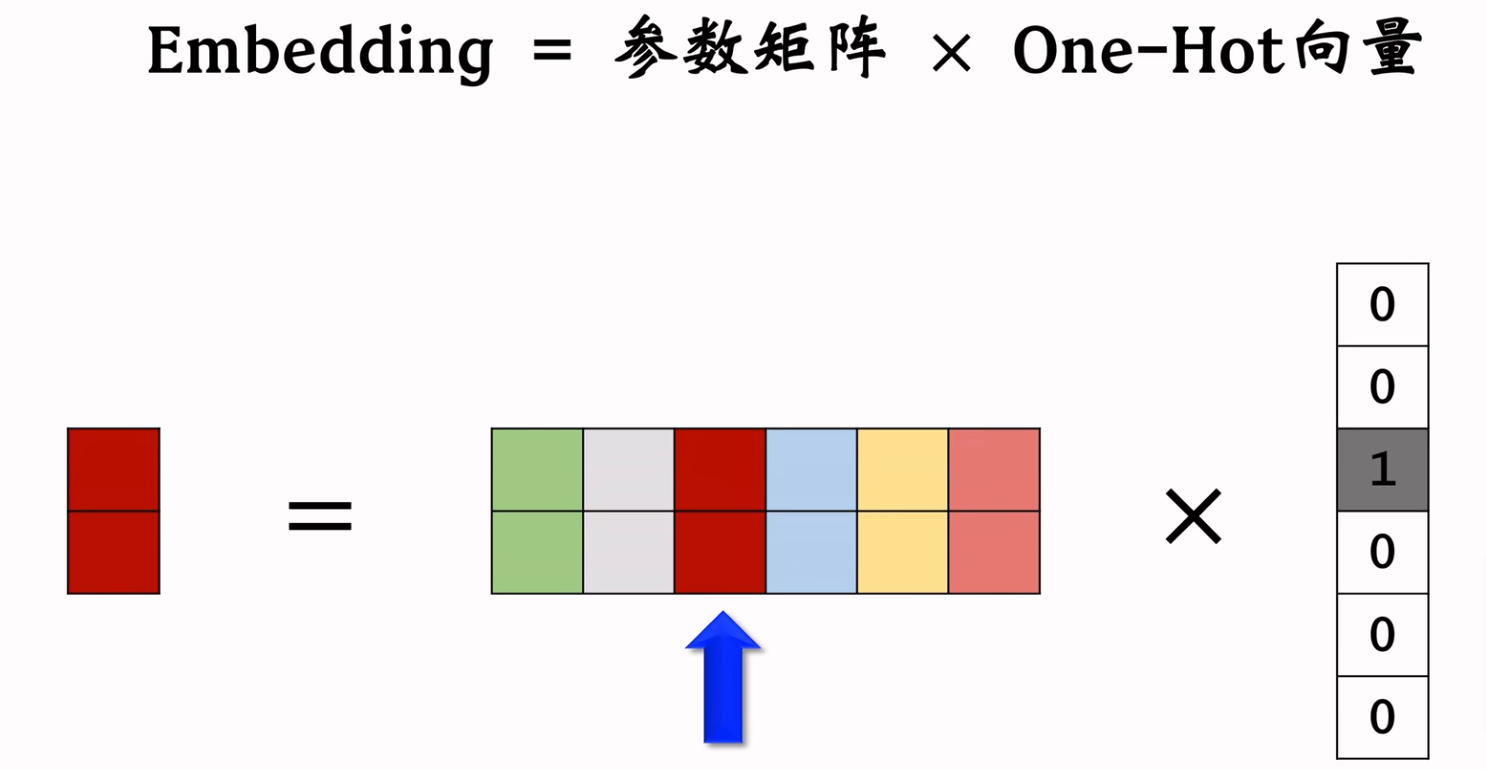
但是当取值个数特别多,比如用户ID、物品ID等,则上述编码方式会使用太多的参数。通常采用Embedding向量化的方式编码,就是给每个取值映射到一个k维向量,维护一个二维矩阵参数表(维度是:向量大小*特征取值个数)。示意图如下:

Embedding使用方式
使用时,假如$国籍=印度(3)$,则从Embedding矩阵参数中取到第3个列向量,其实就是Embedding参数矩阵与特征One-Hot编码向量内积。例如:
特征值$印度$的One-Hot编码为:[0, 0, 1, 0, …, 0],即只有第3个数字为1,其他全为0。那么Embedding参数矩阵与其内积时,就是取其第3列。
参数量对比,以国籍特征200个特征值为例,若使用One-Hot编码方式,则参数量是:200*200=40000个;若使用Embedding方式,每个特征值编码为一个4维向量,则参数量为:200*4=800个。
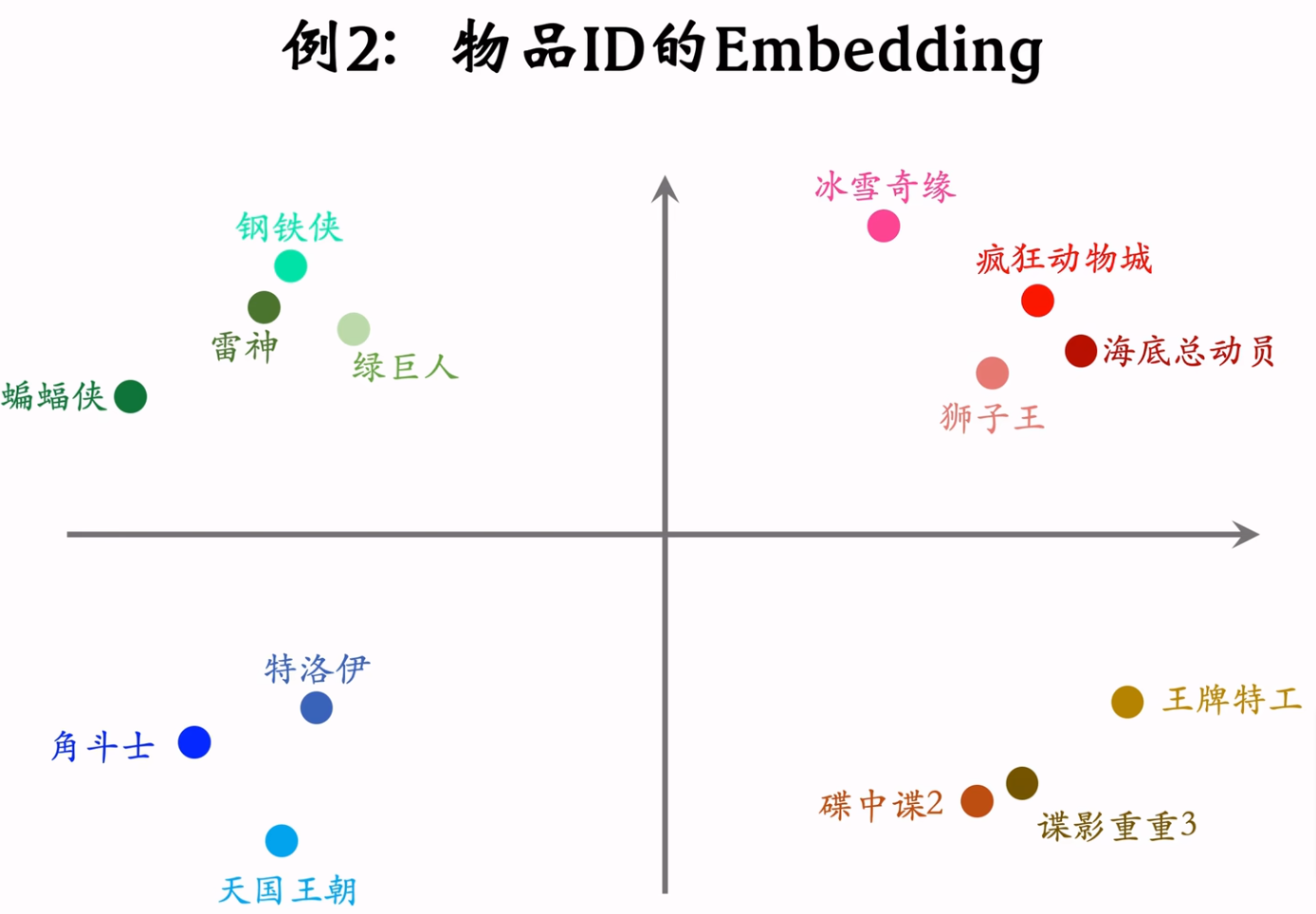
Embedding表示相似度
Embedding还可以表示出两个物品之间的相似度。
矩阵补充召回
原理和训练
矩阵补充结构图如下:
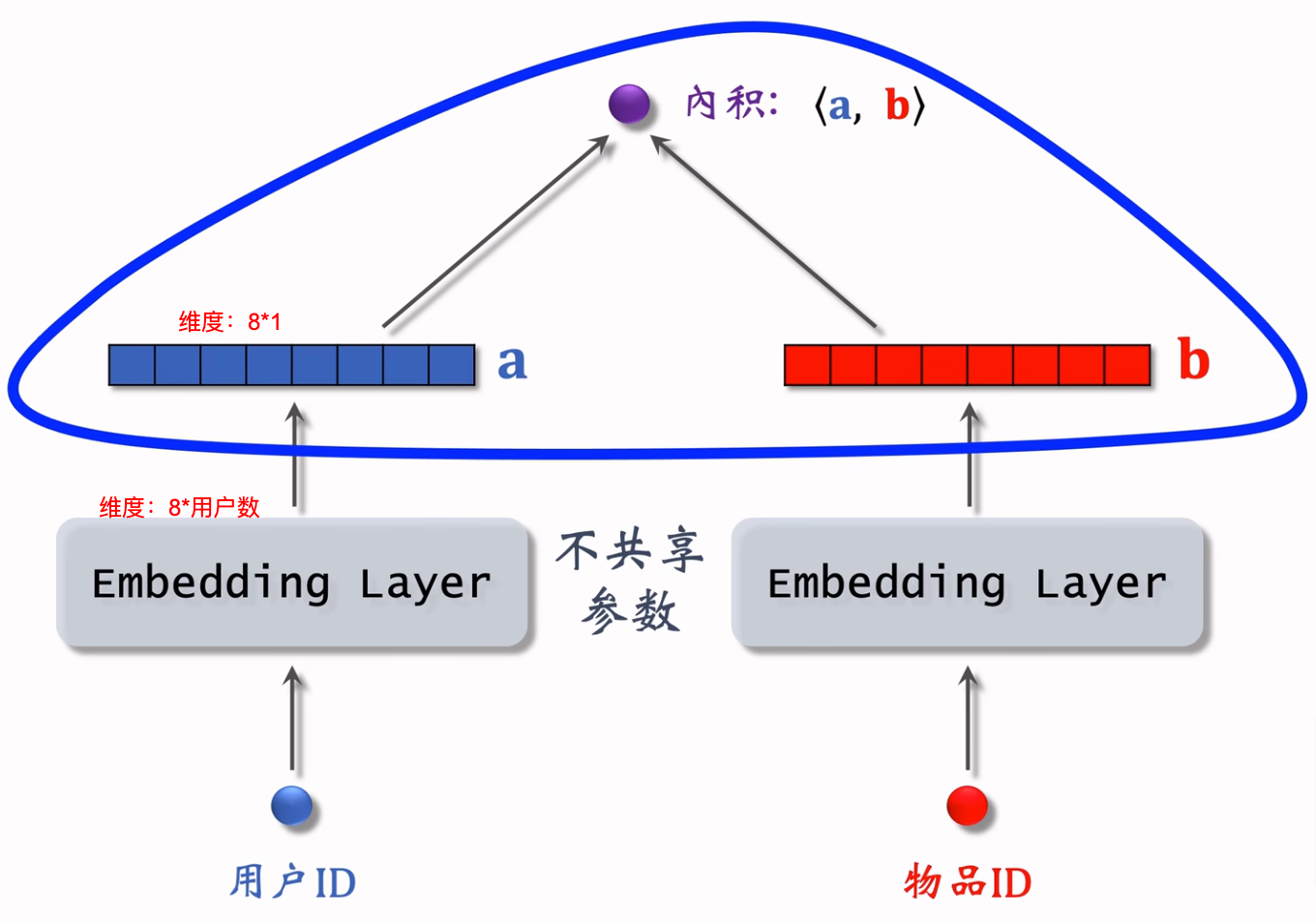
用户和物品的Embedding参数矩阵示意图如下:
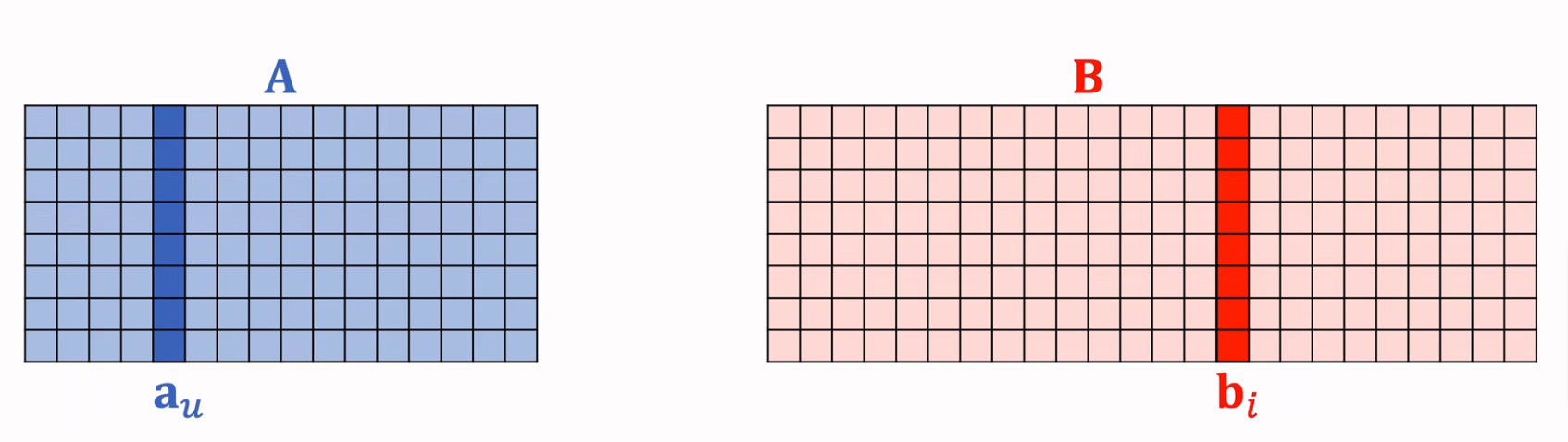
则向量内积$\lt a_u, b_i \gt$可表示用户$u$对物品$i$的兴趣打分。
记训练数据总体为$\Omega$,每一条样本为$(u, i, y)$,表示为$(用户ID,物品ID,兴趣分数)$。则训练的优化目标是:
$$
\underset{A,B}{\min} \sum_{(u,i,y) \in \Omega} (y – \lt a_u, b_i \gt )^2 \tag{7}
$$
在线流程
- 训练用户和物品两个Embedding参数矩阵,并把用户Embedding参数矩阵存储至缓存。
- 给定用户ID,查找其Embedding向量,记作$a$
- 使用最近邻方法从物品Embedding参数矩阵中查找到分数最高的K个物品。
其中第3步中查找K个物品时,如果使用遍历方式,则时间复杂度与物品数量正比,若物品数量巨大,则耗时会非常大,所以需要改进查找方式:近似最近邻查找方法。
近似最近邻查找方法
该方法已经集成到Milvus、Faiss、HnswLib等向量数据库工具中。常用的索引方式包括暴力检索、局部哈希敏感(LSH)、倒排快速索引、乘积量化索引、树索引(TDM)、图索引(HNSW)等等。
衡量最近邻的标准:
- 欧氏距离最小(L2距离)
- 向量内积最大
- 余弦相似度最大
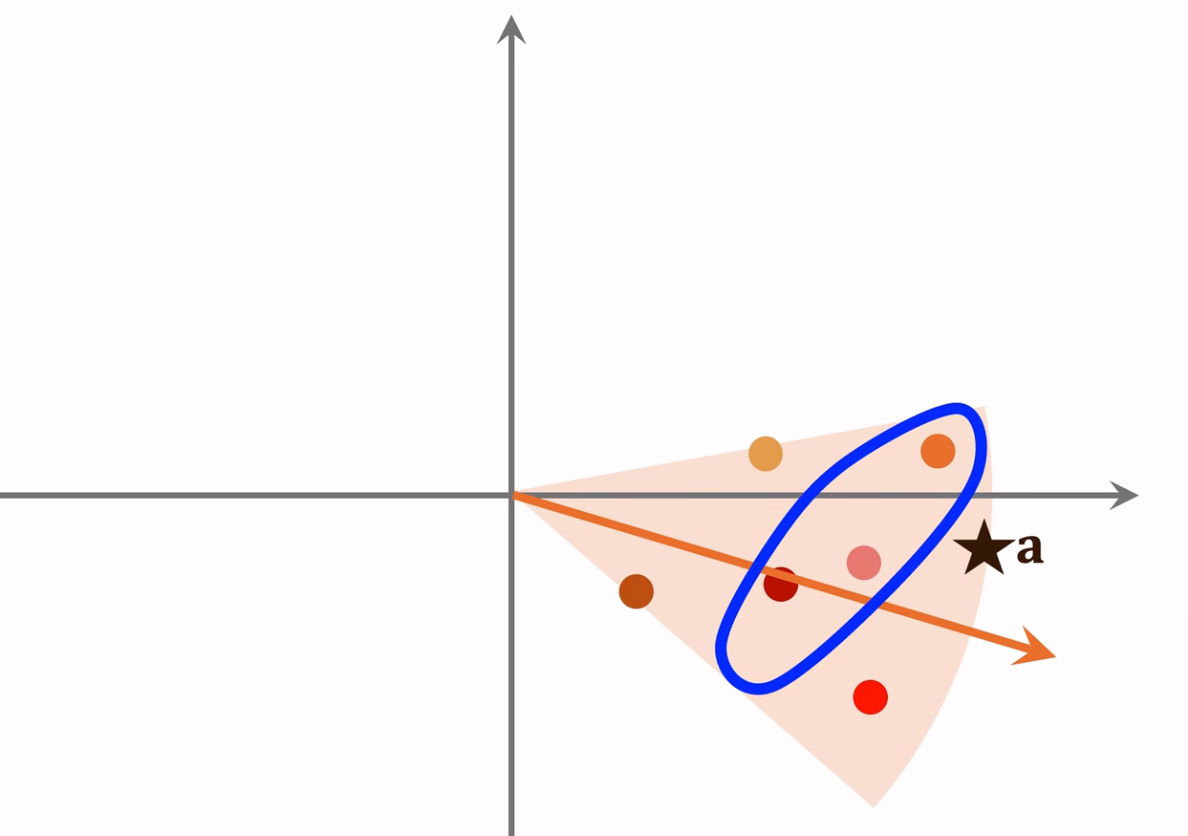
第一步:先把向量聚类,并计算每个类别的平均向量,例如下图中每个扇形表示一个分类。
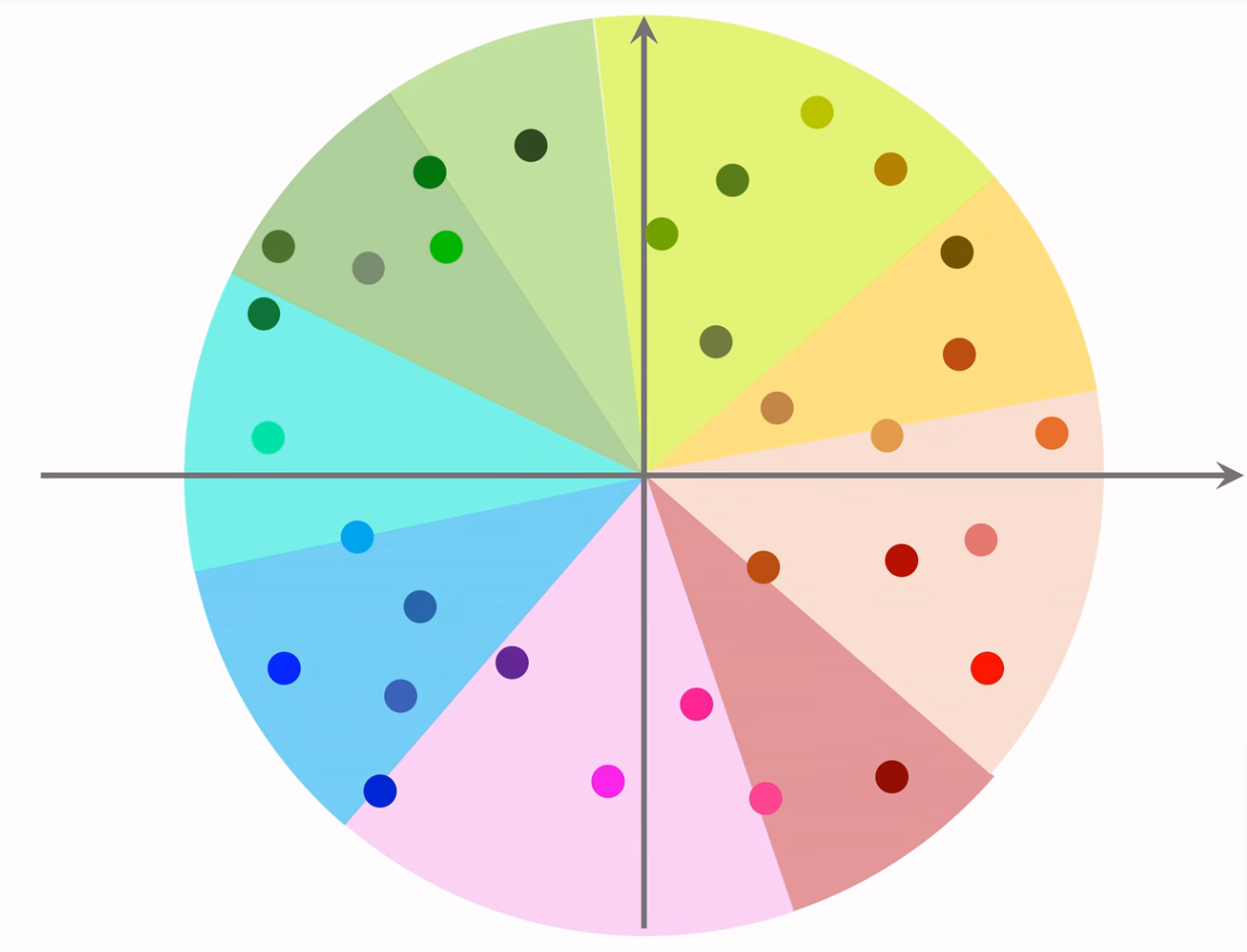
第二步:下图中的每个箭头就是类别平均向量,把这些向量索引到向量数据库。

第三步:给定用户ID,从类别平均向量中,找到最接近的向量(橙色箭头)。然后再根据类别向量索引到属于这个分类的所有物品向量(橙色扇形中的每个点),再逐个计算相似度找到最相近的K个即可(蓝色线圈起来的点)。
问题
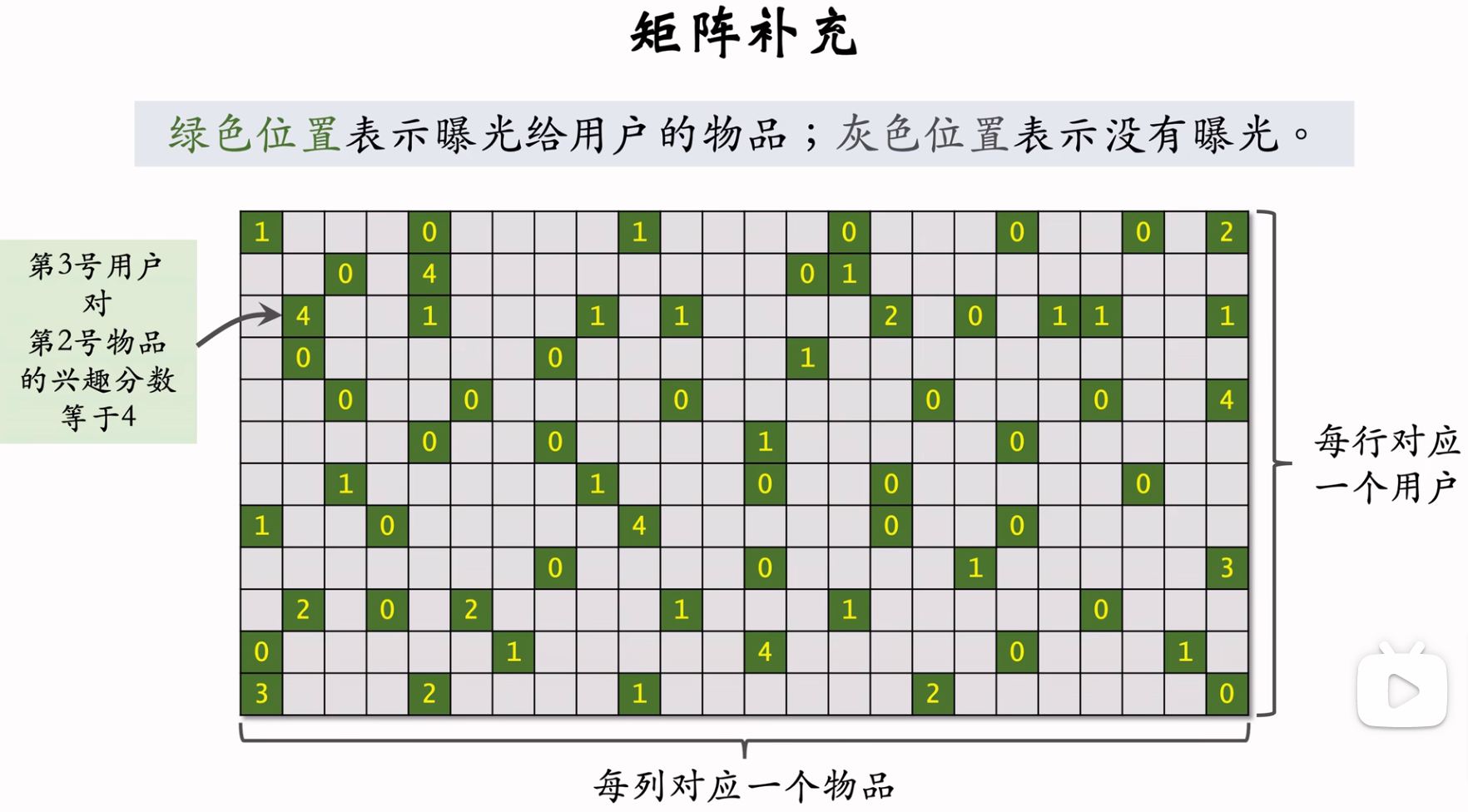
矩阵补充示意图如下,可以看到多数用户和物品之间是没有交互行为记录的,矩阵补充的作用是通过内积的方式把灰色位置补齐。
矩阵补充方法缺点:该方法实际上线效果并不好,原因如下:
- 训练Embedding参数矩阵时,只用了用户和物品ID,没有用到用户和物品的各种属性。
- 负样本的选取方式不对。正样本选取曝光之后有交互的记录没有问题,但是负样本选取的是曝光之后没有交互记录的,这种方式是错误的。具体如何选取负样本,可以参考本文下方的章节《召回的负样本选择方法》。
- 训练方式不好。首先是兴趣分数使用内积(比较两个向量的方向和模长)不如余弦相似度(比较两个向量的方向是否一致)更好;其次平方损失不如交叉熵损失。
双塔模型召回(矩阵补充的改进)
模型结构
双塔模型主要是针对矩阵补充的缺点进行升级。
第一点:用户塔使用了用户ID和其他用户特征,示例如下(物品塔类似):

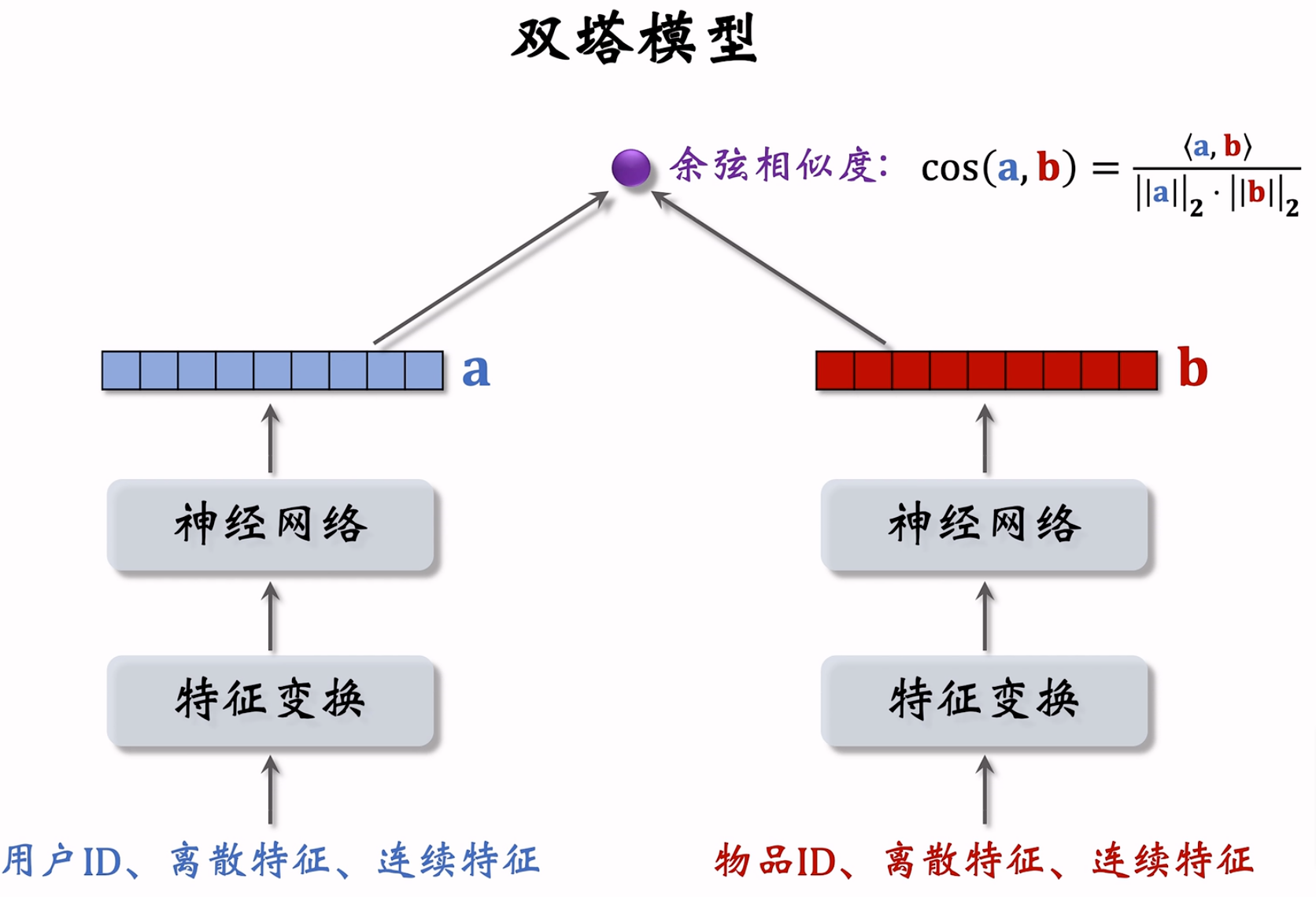
第二点:把内积改为余弦相似度,整个双塔模型结构如下:
模型训练的三种方法
- Pointwise:独立看待每一个正负样本,做简单的二元分类
(1)对于正样本,鼓励$cos(\pmb{a}, \pmb{b}) \rightarrow 1$
(2)对于负样本,鼓励 $cos(\pmb{a}, \pmb{b}) \rightarrow -1$
(3)正负样本比例可控制在1:2或1:3(业界经验值)
- Pairwise:每次取一个正样本、一个负样本组成二元组,参考文献《Embedding-based Retrieval in Facebook Search – 2020》
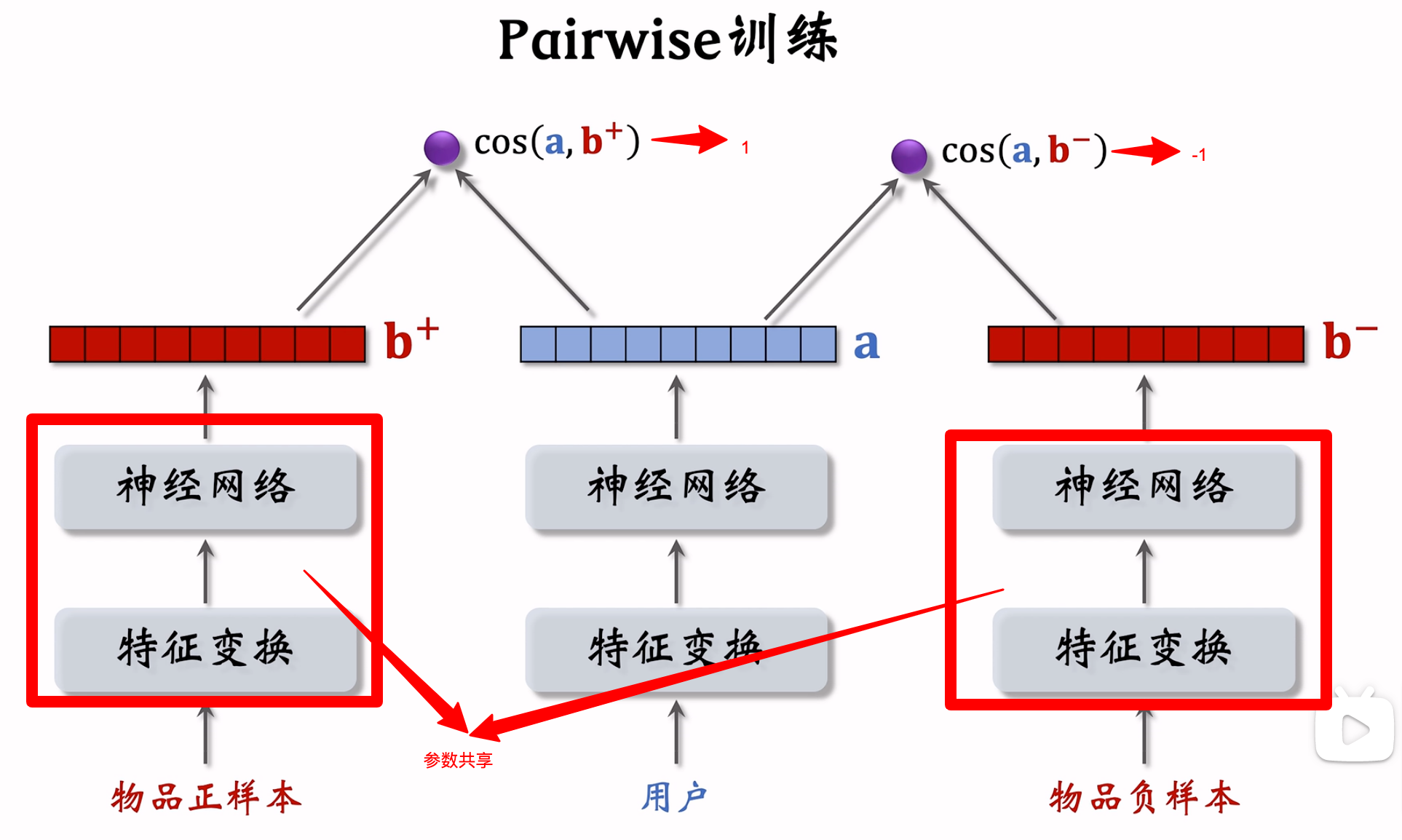

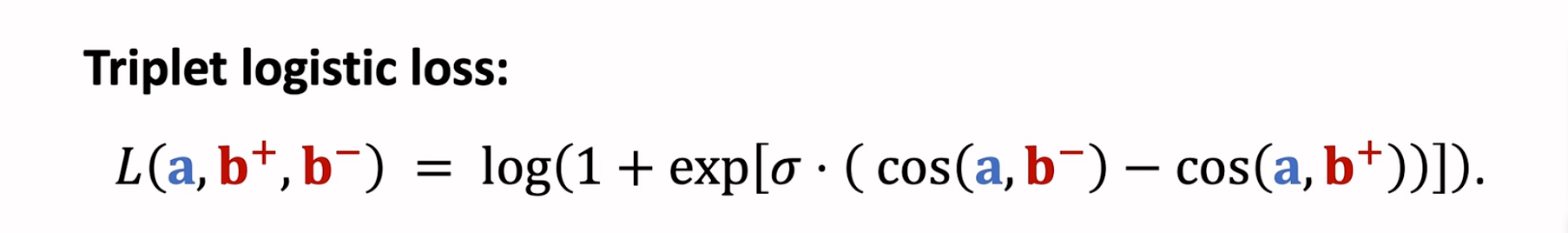
- Listwise:每次取一个正样本、多个负样本组成列表,参考文献《Sampling-Bias-Corrected Neural Modeling for Large Corpus Item Recommendations – 2019》
(1)鼓励$cos(\pmb{a}, \pmb{b^+})尽量大$
(2)鼓励$cos(\pmb{a}, \pmb{b_1^-}),cos(\pmb{a}, \pmb{b_2^-})…cos(\pmb{a}, \pmb{b_n^-}) 尽量小$

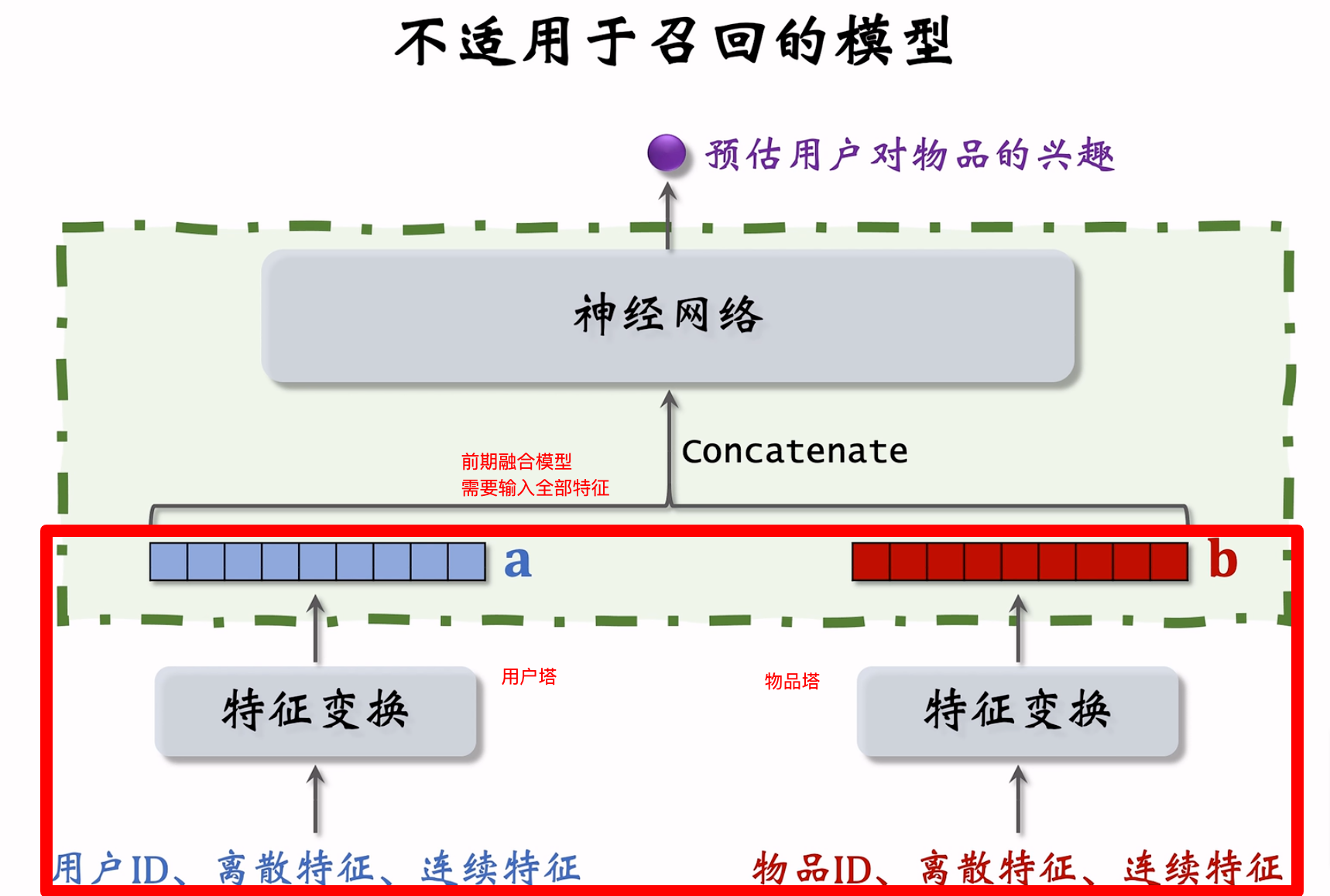
不适用于召回的模型结构(前期融合)
下述模型结构,虽然也有用户塔和物品塔,但是用户和物品向量在神经网络之前融合(称为前期融合),不适用于召回问题。因为在线时需要输入用户和物品的所有特征。
而召回双塔模型,采用的是把用户和物品塔分别经过神经网络层后的向量进行融合(后期融合),再计算余弦相似度,这样在线时,就可以根据用户ID和物品ID获取到表征向量。
召回的负样本选择方法
- 简单负样本-全体:全体样本随机挑选。那么挑选概率如何设定?均匀抽样还是非均匀抽样?
(1)均匀抽样:对冷门物品不公平,因为冷门物品在样本中占比较低。
(2)非均匀抽样:打压热门物品,与热门程度呈正相关。比如:$抽样概率 ∝ (点击次数)^{0.75}$
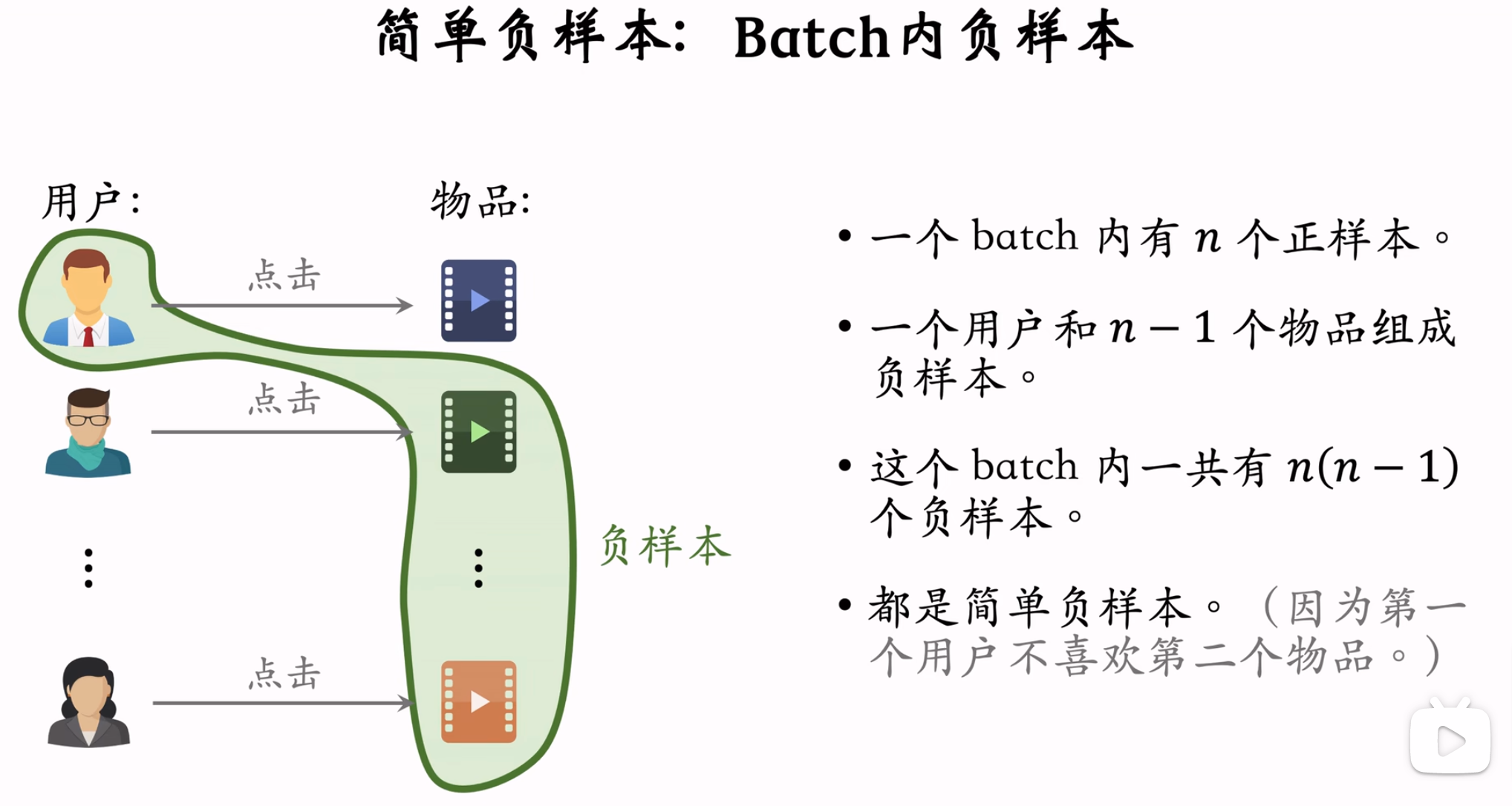
- 简单负样本-Batch内:用户与Batch内其他记录的物品组成样本对,但是这样的话,$抽样概率 ∝ 点击次数$,导致热门物品成为负样本的概率比较大,因此需要纠偏,参考下面第2张图。

- 困难负样本有两类
(1)被粗排淘汰的物品(比较困难),容易分错。
(2)精排分数靠后的物品(非常困难,因为这些物品与用户的兴趣非常接近了),非常容易分错。
-
工业界做法:混合几种负样本方法,比如50%简单样本,50%困难样本。
-
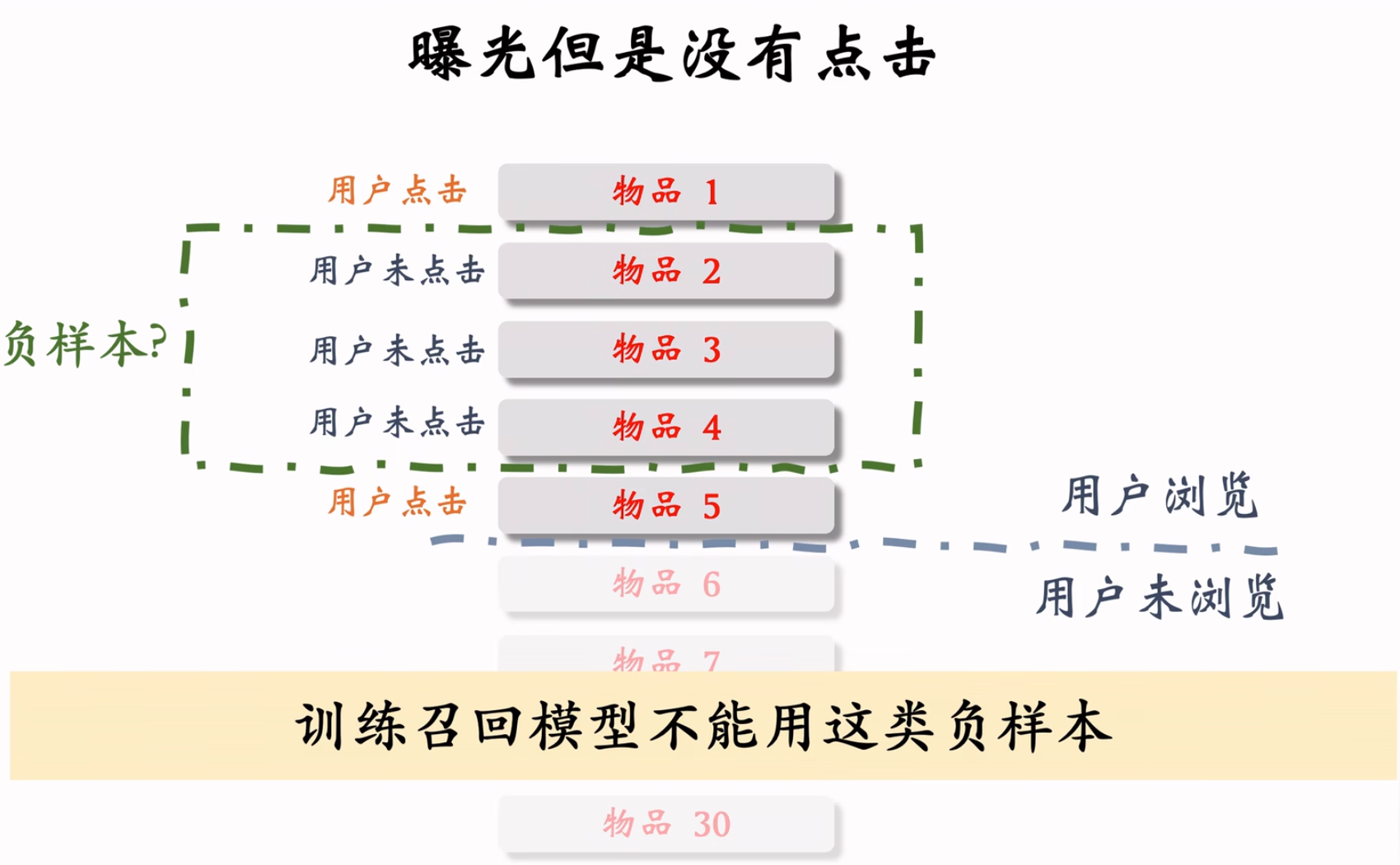
重点:曝光未点击不能作为召回负样本,可以作为排序的负样本。召回的目标是:区分用户对物品是可能感兴趣和不感兴趣。排序的目标是:区分用户对物品是比较感兴趣和非常感兴趣。
双塔模型改进-自监督学习
双塔模型问题
-
推荐系统头部效应严重,即少数物品占了大部分点击,大部分物品点击次数不高。
-
高点击的物品表征学习较好,长尾物品的表征学的不够好。
自监督学习
-
目标:更好的学习长尾物品的表征,参考文献《Self-supervised Learning for Large-scale Item Recommendations》和知乎文章《对比学习-推荐系统:Self-supervised Learning for Large-scale Item Recommendations》。
-
自监督学习原理:鼓励$cos(b_i^{‘}, b_i^{”})$尽量大,鼓励$cos(b_i^{‘}, b_j^{”})$尽量小
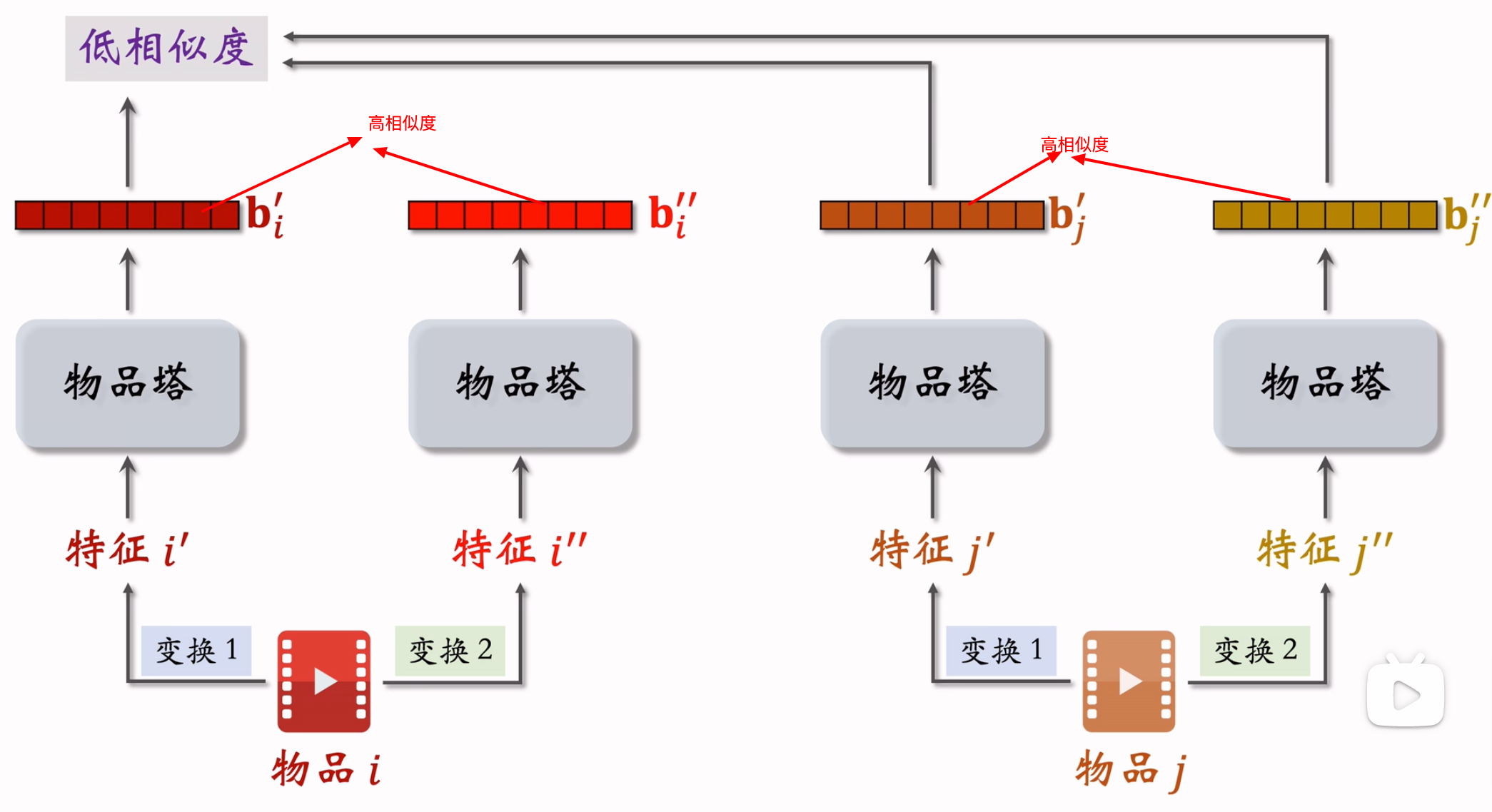
- 特征变换
(1)Random Mask:随机选择一些特征,把他们遮住,置为default取值。
(2)Dropout:随机选择一些特征,丢掉50%的取值,例如$u={美妆,摄影} \rightarrow {美妆}$
(3)互补特征(complementary):

(4)Mask一组关联的特征。
- 自监督学习损失函数:
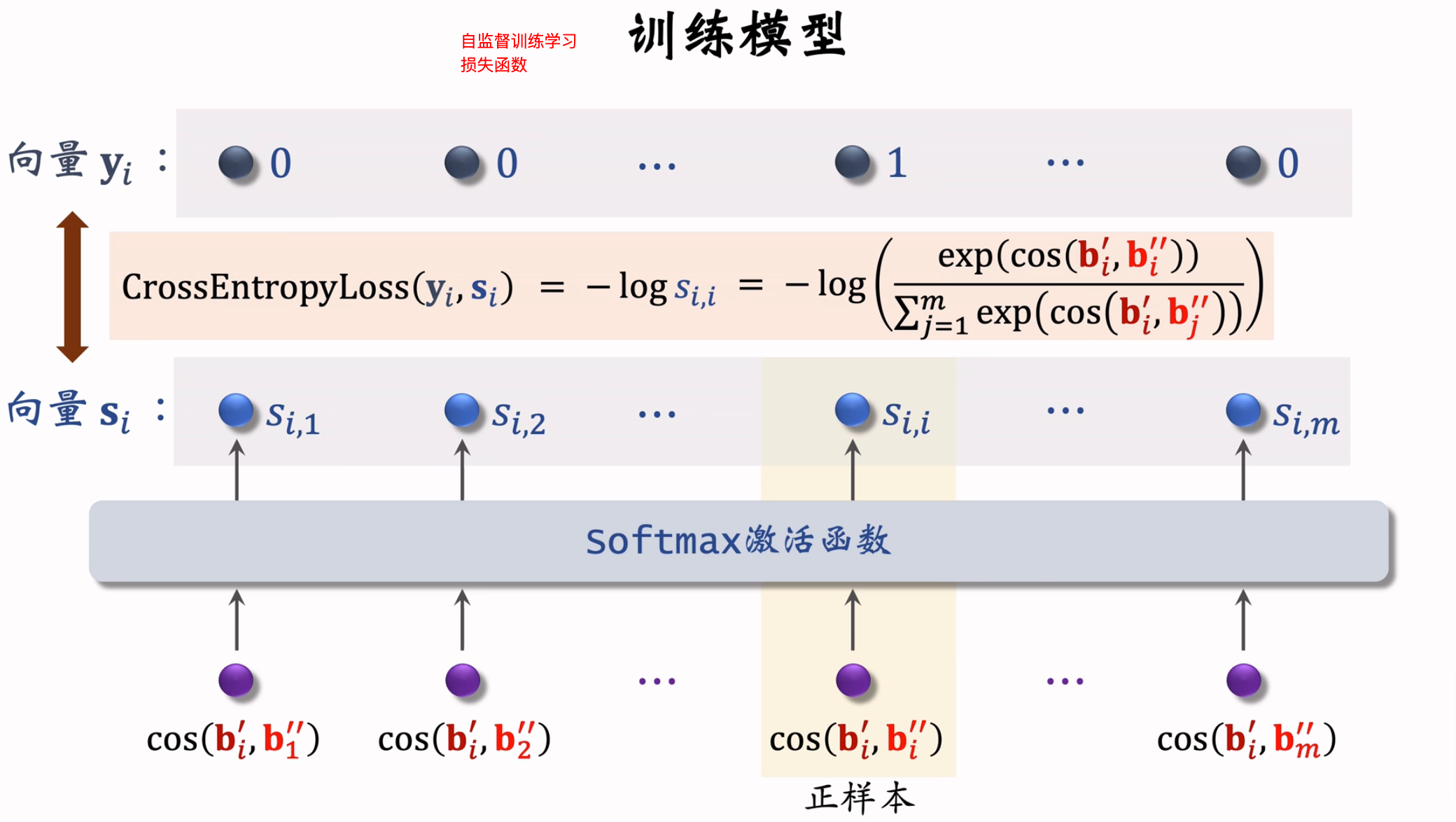
双塔模型+自监督学习的损失函数
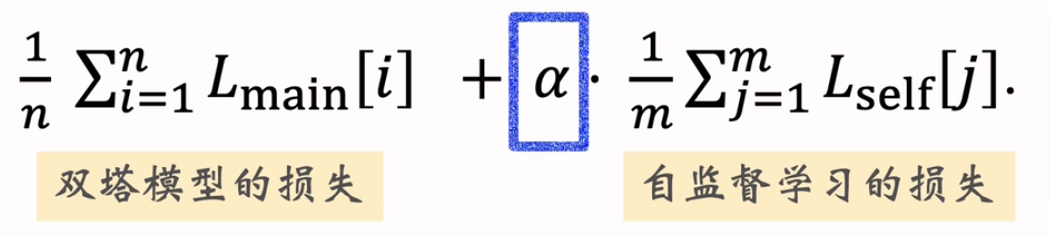
其他召回通道
位置召回
- GeoHash召回
- 同城召回
作者召回
- 有交互的作者
- 关注的作者
- 相似的作者
缓存召回
参考文献
公开课地址:GitHub
本文永久更新地址: https://notlate.cn/p/07689bd69c9a0a6f/
评论