机器学习需要弄清楚的知识点记录
|
823
|
0
|
知识点

本文主要记录一下学习推荐模型需要弄清楚的基础概念和知识点汇总，更全面的知识推荐阅读书籍：

  • 《统计学习方法 第2版》- 李航 著
  • 《程序员的数学2 概率统计》- 平冈和幸 堀玄 著
  • 《程序员的数学3 线性代数》- 平冈和幸 堀玄 著

概率

概率分布（单个随机变量）

随机事件数量化之后称为随机变量，随机变量分为离散型和连续型。关于概率分布，可以阅读百科《概率分布函数》。总结来说就是：

  1. 离散型随机变量的概率分布是$P(X=x_i) = p_i$ ，$i = 1,2,3…$，其概率分布函数为$F(x) = \sum_{x_i<n}p_i$

  2. 连续型随机变量需要用概率密度函数$f(x)$刻画概率分布规律，其概率分布函数为$F(x) = \int_{-\infty}^x f(x) dx $ ，即$f(x)$是$F(x)$的导数。注意：$f(x)$表示的不是面积，要计算X落在某个区间$[x_1, x_2]$的概率，则表示为

$$
P(x_1≤X≤x_2)=F(x_2) – F(x_1) = \int_{x_1}^{x_2} f(x) dx \tag{1}
$$

联合概率（多个随机变量）

常见的监督学习，即有明确的输入和真实值，可表示为随机变量$X$和$Y$，通常假设其遵循联合分布概率$P(X, Y)$，也就是表示这多个事件同时发生的概率。

条件概率

设$A$和$B$是样本空间中的两个事件，在$B$发生的条件下，$A$发生的条件概率为：$P(A|B) = \frac{P(A, B)}{P(B)}$。

贝叶斯公式

贝叶斯定理是描述在已知一些条件下，某事件的发生机率。通常，事件A在事件B已发生的条件下发生的机率，与事件B在事件A已发生的条件下发生的机率是不一样的。然而这两者是有确定的关系的，贝叶斯定理就是这种关系的陈述。其公式为：
$$
P(A|B) = \frac{P(A)P(B|A)}{P(B)} 或 P(\theta|X) = \frac{P(\theta)P(X|\theta)}{P(X)} \tag{2}
$$
公式中每个部分都有约定俗称的名称：

  • $P(A|B)$是已知$B$发生后，$A$的条件概率，称为$A$的后验概率
  • $P(A)$是$A$的先验概率(或边缘概率)
  • 同样的，$P(B|A)$是$B$的后验概率，又称为$A$的似然函数。即$P(B|A) = L(A|B)$，下面参数估计会用到。
  • $P(B)$是$B$的先验概率

综上可得：
$$
后验概率 = \frac{先验概率 * 似然函数}{标准化常量} \tag{3}
$$

共轭先验和共轭分布

举个例子快速了解，公式$(3)$中的分母是一个常量，忽略后，可近似得到以下公式：
$$
后验概率 = \frac{先验概率 * 似然函数}{标准化常量} \propto 先验概率 * 似然函数 \tag{4}
$$
若似然函数服从二项分布，先验概率服从Beta分布，根据上式计算出的后验概率也会服从Beta分布（可参考文章的推导），那么就说二项分布和Beta分布属于共轭分布，先验概率是似然函数的共轭先验。

全概率公式

不严谨的介绍：假设事件$B$的取值为$1,2,3,…,n$。则对任意事件$A$有全概率公式：

$$
P(A) = P(A, B_1) + P(A, B_2) + … + P(A, B_n)=\sum_{i=1}^nP(A, B_i) \tag{5}
$$
又根据条件概率可得$P(A, B)=P(A|B_n)P(B_n)$，所以全概率公式可写为：
$$
P(A)=\sum_{i=1}^nP(A|B_i)P(B_i) \tag{6}
$$
可以把贝叶斯公式中的$P(B)$按照全概率公式展开得到一个经常使用的形式（离散型随机变量）：

$$
P(A_i|B) = \frac{P(B|A_i)P(A_i)}{P(B)} = \frac{P(B|A_i)P(A_i)}{\sum_{i=1}^nP(B|A_i)*P(A_i)} \tag{7}
$$
若是连续型随机变量，则$\sum$需要改为$\int$。

参数估计

根据从总体中抽取的随机样本来估计总体分布中未知参数的过程。介绍三种常用的估计方法。

最大似然估计

思想：认为待估计分布的参数$\theta$是确定的，只是未知而已，认为使得观测数据发生概率$P(X|\theta)$最大的参数就是最好的参数。

已知一个概率分布$D$的概率密度函数（连续分布）或概率质量函数（离散分布）为$f_D$，以及一个分布参数$\theta$。我们可以从这个分布中抽$n$个采样$X_1, X_2, … ,X_n$，然后利用$f_D$计算出似然函数：

$$
L(\theta|x_1, x_2, … , x_n) = P(x_1, x_2, … , x_n|\theta) = f_\theta(x_1, x_2, … , x_n) \tag{8}
$$
若从$D$中抽取的样本集是独立同分布的，则上式可继续化简为多个条件概率连乘：

$$
L(\theta|x_1, x_2, … , x_n) = \prod_{i=1}^nL(\theta|x_i) = \prod_{i=1}^nP(x_i|\theta)=\prod_{i=1}^nf_\theta(x_i) \tag{9}
$$
似然函数的含义是：若$D$是离散分布，$f_\theta$表示参数为$\theta$时观测到这一采样的概率。若$D$是连续分布，$f_\theta$为$X_1, X_2, … ,X_n$联合分布的概率密度函数在观测值处的取值。

最大似然估计就是在$\theta$所有可能的取值中，寻找一个$\hat\theta$使得似然函数取到最大值，$\hat\theta$就称为$\theta$的最大似然估计。表示为：

$$
\hat\theta_{最大似然}(x) = \underset{\theta}{\operatorname{argmax}} f_\theta(x) \tag{10}
$$
为了便于计算最大值，通常取似然函数的对数，即把连乘改成连加，因为对数函数是单调的，所以不改变原似然函数单调性：

$$
log[L(\theta|x_1, x_2, … , x_n)] = log[\prod_{i=1}^nP(x_i|\theta)] = \sum_{i=1}^nlog[P(x_i|\theta)] = \sum_{i=1}^n log[f_\theta(x)] \tag{11}
$$
接下来可以通过求导计算出$\theta$的极值。

最大似然估计的注意点：

  • 概率分布必须已知
  • 似然函数指的是$x_1, x_2, … , x_n$是常量，$\theta$是变量的函数
  • 最大似然估计不一定存在，也不一定唯一

最大后验概率估计

思想：认为待估计分布的参数$\theta$是个随机变量，也就是$\theta$具有某种概率分布（称为先验概率分布）。认为使得参数$\theta$的后验概率最大的$\theta$就是最好的。

回顾贝叶斯公式和共轭先验一节，$\theta$的后验概率可用公式$(4)$表示，即

$$
P(\theta|X) = \frac{P(\theta)P(X|\theta)}{P(X)} \propto P(\theta)P(X|\theta) = g(\theta)*f_\theta(x) \tag{12}
$$
这是由于$P(X)$与参数$\theta$无关。其中$P(\theta)$是$\theta$的先验概率，也可表示为$g_D$；$P(X|\theta)$是$X$的后验概率或似然函数，可表示为$f_D$。从上式可以看出，最大后验概率估计相比最大似然估计，就是多考虑了参数$\theta$的先验概率。

同样可以通过求导的方法计算出最好的$\theta$，可表示为：

$$
\hat\theta_{最大后验概率}(x) = \underset{\theta}{\operatorname{argmax}} f_\theta(x) * g(\theta) \tag{13}
$$
若对后验概率取对数可得：
$$
\hat\theta_{最大后验概率}(x) = \underset{\theta}{\operatorname{argmax}} log[f_\theta(x) * g(\theta)] = \underset{\theta}{\operatorname{argmax}}[log(f_\theta(x)) + log(g(\theta))] \tag{14}
$$
如果把$log(g(\theta))$看作是结构风险中的正则化项，则最大后验概率估计可以看作是规则化的最大似然估计。

最大后验概率估计注意点：

  • 若$g(\theta)$为常数函数时，最大后验概率估计 与 最大似然估计 重合
  • 参数$\theta$的先验概率分布需要事先确定

贝叶斯估计

贝叶斯估计是最大后验概率估计的扩展。

思想：同样认为待估计分布的参数$\theta$是一个随机变量，最大后验概率估计是估计出参数$\theta$的某个特征值，而贝叶斯估计是直接估计$\theta$的概率分布。

再把贝叶斯公式$(2)$写一遍：$P(\theta|X) = \frac{P(\theta)*P(X|\theta)}{P(X)}$。在最大后验概率估计中，因为与$\theta$无关而忽略了先验概率$P(X)$，但是在贝叶斯估计中，$P(X)$是不可忽略的。若$X$是连续随机变量，根据全概率公式可得：

$$
P(X) = \int_{\theta取值空间}P(X|\theta)P(\theta)d\theta \tag{15}
$$
所以贝叶斯公式改写为：
$$
P(\theta|X) = \frac{P(X|\theta)P(\theta)}{\int_{\theta取值空间}P(X|\theta)P(\theta)d\theta} \tag{16}
$$
实际使用时，因为计算全概率公式的积分非常困难，所以需要用到共轭先验。大概思路如下：

  • 在最大后验概率估计中，参数$\theta$的先验概率$P(\theta)$的概率分布需要事先确定，在贝叶斯估计中也同样如此
  • 由于假设先验概率$P(\theta)$是似然函数$P(X|\theta)$的共轭先验，那么似然函数$P(X|\theta)$的概率分布也可以确定

  • 当先验概率分布$P(\theta)$和似然函数$P(X|\theta)$的概率分布都确定后，就可以带入贝叶斯公式求解后验概率$P(\theta|X)$的概率分布

  • 由于后验概率分布是一个条件分布，通常取后验概率分布的期望作为参数$\theta$的估计值

统计学习三要素

按照《统计学习方法》开篇中介绍的，统计学习方法的三要素是：模型、策略和算法。即从全体模型（假设空间）中选取一个最优模型，使它对已知的训练数据和未知的测试数据在给定的评价准则下有最优的预测。其中模型选择的准则是策略，求解最优模型的是算法。

模型

按照不同的维度，可以有不同的分类。比如按照学习方式可以分为监督学习、无监督学习等；按照模型种类可以分为概率模型（学习的是条件概率分布$P$）和非概率模型（学习的是函数映射关系$f$）。综合这两种分类，我们可以总结模型表示如下：

监督学习 + 概率模型 = 生成模型

要学习的模型可表示为条件概率$P(Y|X)$；

通过给定的训练集学习联合概率$P(X, Y)$，然后根据先验概率$P(X)$，得到一个最优模型，表示为$\hat{P}(Y|X)$；

当用最优模型对具体输入进行输出预测时，可表示为
$$
y_{N+1} = \underset{y}{\operatorname{argmax}} \hat{P}(y|x_{N+1}) \tag{17}
$$
其中$\underset{y}{\operatorname{argmax}}$表示从模型输出的$y$的概率分布表（也就是$y$的所有取值以及对应的概率）中，选择概率最大的取值。

监督学习 + 非概率模型 = 判别模型

要学习的模型可表示为决策函数$Y=f(X)$；

通过给定的训练集直接学习决策函数$f(X)$，得到一个最优模型，表示为$Y = \hat{f}(X)$;

当用最优模型对具体输入进行输出预测时，可表示为$y_{N+1}=\hat{f}(x_{N+1})$。

无监督学习 + 概率模型

要学习的模型表示为：条件概率$P(Z|X)$（用于聚类或降维）或$P(X|Z)$（用于概率估计），其中$X$表示输入，$Z$表示输出。

学习后的最优模型表示为：条件概率$\hat{P}(Z|X)$或$\hat{P}(X|Z)$

预测时，可表示为：$z_{N+1} = \underset{z}{\operatorname{argmax}} \hat{P}(z|x_{N+1})$或$\hat{P}(x_{N+1}|z_{N+1})$给出输入的概率

无监督学习 + 非概率模型

要学习的模型表示为：函数$Z = g(X)$

学习后的最优模型表示为：函数$Z = \hat{g}(X)$

预测时，可表示为：$z_{N+1} = \hat{g}(x_{N+1})$

策略

策略就是按照什么样的准则学习或选择最优的模型。

各种学习函数名词梳理

  • 损失函数：定义在单个样本上的，计算单个样本的误差。
  • 代价函数：定义在整个训练集上的，是所有样本误差（损失函数）的平均
  • 期望风险函数（期望损失）：理论上模型的平均损失，学习的目标就是选择期望风险最小的模型。
  • 经验风险函数（经验损失）：实际上模型在训练集上的平均损失，根据大数定律，当训练集趋于无穷时，风险风险趋于期望风险。

  • 结构风险函数：在经验风险上加上表示模型复杂度的正则化项（regularizer）或惩罚项（penalty term）。

  • 经验风险函数最小化：就是求解代价函数最小化，当样本足够多时，往往有好的学习效果。比如极大似然估计。

  • 结构风险函数最小化：当样本不够多时，经验风险最小学习效果未必很好，会产生过拟合现象。结构风险最小化是为了防止过拟合而提出来的策略，等价于正则化，其作用是降低模型复杂度，减轻过拟合。比如最大后验概率估计。
  • 目标函数：最终需要优化的函数，等于 经验风险+结构风险，也就是 代价函数+正则化。

综上，监督学习问题变成了经验风险或结构风险函数的最优化问题。

常用的损失函数有如下几种：

  • 0-1损失函数：即模型预测结果与真实值相同则为损失为0，否则损失为1.
  • 平方损失函数：误差的平方
  • 绝对损失函数：误差的绝对值
  • 交叉熵损失函数：主要用于衡量两个分布（预测分布和实际分布）之间的差异。
  • 对数损失函数或对数似然损失函数：误差的负对数，通常用于概率模型。这是一个通用的损失函数：如果把它应用于服从伯努利分布的数据时，对数损失函数等价于交叉熵损失函数；如果把它应用于服从高斯分布的数据时，对数损失函数等价于平方损失函数；如果把它应用于服从拉普拉斯分布的数据时，对数损失函数等价于绝对损失函数。

更多信息可以阅读《常见的损失函数(loss function)总结》。

算法

算法是指学习模型的具体计算方法，也就是考虑用什么样的计算方法求解最优模型，可以归结为最优化问题。

  • 解析解：如果最优化问题比较简单，可以直接通过严格的公式所求得。
  • 数值解：通常机器学习最优化问题的解析解不存在，这就需要用数值计算的方法求解，如何快速高效地找到全局最优解是一个重要的问题。

常用的优化算法

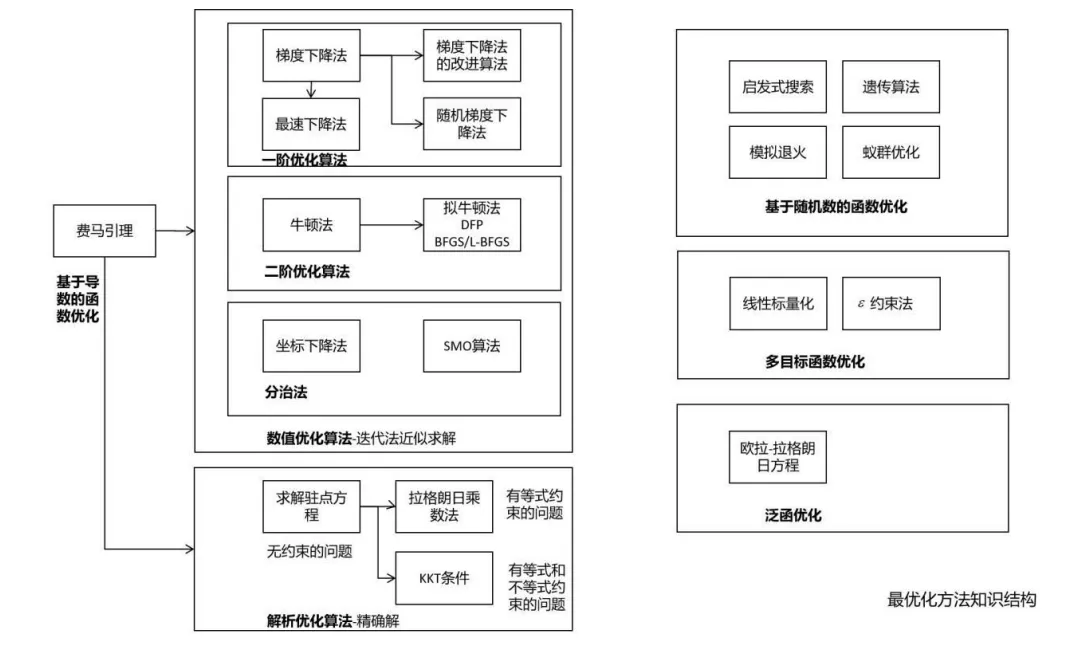
最优化方法知识结构

主要记录几个常用的：

  • 费马定理：不带约束的极值问题，也就是熟知的导数等于0的点就是极值点，但这是必要不充分条件
  • 拉格朗日乘数法：带等式约束的极值问题，在极值点处对自变量和乘子变量的导数均需为0，常用于以下方法：
  • 主成分分析
  • 线性判别分析
  • 隐马尔可夫模型
  • KKT条件：同时带有等式和不等式约束的极值问题
  • 梯度下降法：需要计算全部样本的损失，效率低
  • 随机梯度下降法：使用单样本或批样本的损失更新权重，效率高
  • 分治法：一种求解思想，每次迭代只调整优化向量X的一部分分量，其余固定不动

梯度下降法又有多种优化：

  • 动量项：加快梯度下降法的收敛速度，减少震荡，累积了之前的梯度值，等于上次动量项与本次梯度值的加权和
  • AdaGrad：每个分量一个学习率，累加所有历史梯度平方和开根号。缺点：人工设置全局$\alpha$，时间长了趋于$0$
  • RMSProp：改进AdaGrad，衰减历史梯度平方和之后再累加，避免了时间长趋于$0$的问题。缺点：人工指定全局$\alpha$
  • AdaDelta：改进AdaGrad，去掉人工设置参数，避免长期累计趋于$0$
  • Adam：整合了自适应学习率和动量项

其他的可以阅读文章《机器学习中的最优化算法总结》

AUC的含义和计算方式

可以从两个角度理解AUC：

解释1：ROC曲线下面积

先了解预测结果的四种情况：

实际值 – 正 实际值 – 负
预测值 – 正 $TP$ $FP$
预测值 – 负 $FN$ $TN$

总共有$TP$、$FP$、$FN$、$TN$四种结果，第一个字母表示是预测对了（$True$）还是错了（$False$），第二个字母表示预测值是正（$Positive$）还是负（$Negative$）。

$TPR = \frac{TP}{TP + FN}$，表示在所有的正样本$(TP+FN)$中，被正确地预测为正$(TP)$的比例。

$FPR = \frac{FP}{FP + TN}$，表示在所有的负样本$(FP+TN)$中，被错误地预测为正$(FP)$的比例。

ROC曲线的纵轴是$TPR$，横轴是$FPR$。

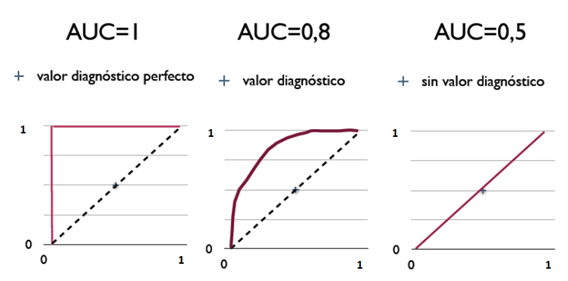
三个AUC取值对应的ROC曲线

我们假设模型的预测值大于阈值，则预测为正，反之预测为负。则：

  • 当阈值非常大，大于模型所有预测的值时，预测结果全是负，即$TP=FP=0$，则$FPR=TPR=0$，即ROC曲线的左下角$(0, 0)$点
  • 当阈值非常小，小于模型所有预测的值时，预测结果全是正，即$FN=TN=0$，则$FPR=TPR=1$，即ROC曲线的右上角$(1,1)$点
  • 随着阈值的变化，模型预测的四种结果随之变化，就可以计算出不同的$TPR$和$FPR$，也就画出了ROC曲线。
  • 当模型预测的非常准时，ROC曲线则越靠近左上角的$(0, 1)$点，比如AUC=1的曲线。

AUC偏左偏右比较

假设上图中红线和蓝线的AUC一样，那么在线效果那种更好呢？

我们实际工作中发现红线的凸起偏向模型预估低分区间，也就是对点击率偏小的样本更准确；蓝线的凸起偏向模型预估高分区间，也就是对点击率较大的样本更准确。因为点击率本身比较小，所以我们在线更喜欢红色曲线。

解释2：随机给一个正样本和负样本，AUC表示有多大的概率把正样本排在负样本之前

这种解释最容易理解，计算也很简单。用模型计算全部$K$个样本的预测值，把所有预测值降序排列；然后从最大值开始编号为$rank=K$，依次递减至最后一个样本的编号为$rank=1$。则只需要统计真实的正样本排在真实的负样本之前的个数占总样本组合对数的比例即可。

假设$K=M+N$，即$M$个实际正样本，$N$个实际负样本。则总共可以组合出$M*N$个样本对。那这里边有多少个样本对是正样本排在负样本之前呢？有个简单办法就是利用最开始的编号。

假设编号为$rank=S$的样本为正样本，则它可以与编号$rank<S$的负样本组合出的有效样本对数，最多是$S-1$个（后边全是负样本），最少是$0$个（后边全是正样本）。

这样先把全部正样本的编号累加求和，就可以组合出全部是正样本开头的样本对。再剔除掉结尾样本也是正样本的情况（公式$(18)$），这有多少个呢？一共是公式$(19)$个。
$$
(M, M), (M, M-1), (M, M-2), … ,(M, 1), (M-1, M-1), … ,(M-1, 1), … , (1,1) \tag{18}
$$

$$
M + (M – 1) + (M – 2) + … + 1 = \frac{M*(M+1)}{2} \tag{19}
$$

所以：
$$
AUC = \frac{\sum_{i∈正样本}rank_i – \frac{M*(M+1)}{2}}{M * N} \tag{20}
$$

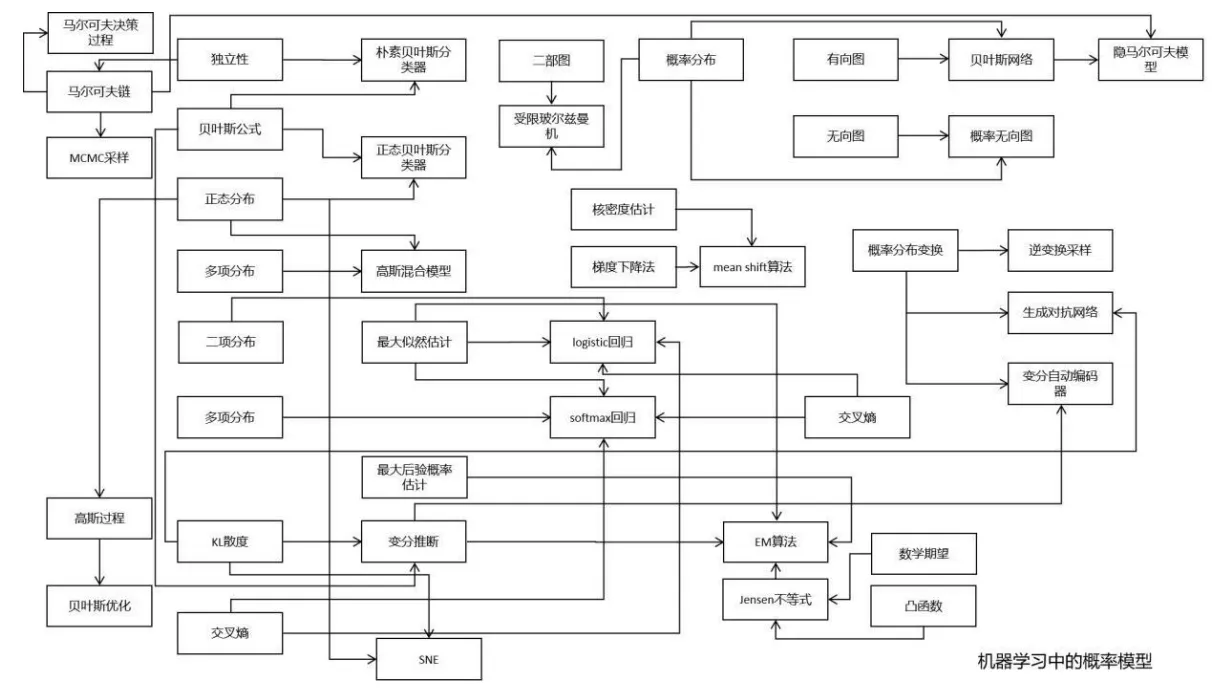
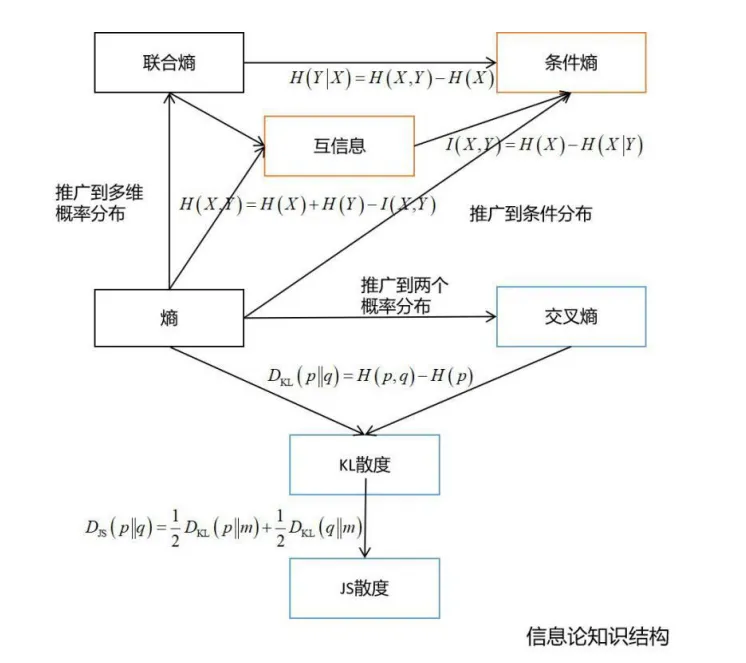
最后贴几张全景图

下述图片来自于文章《机器学习数学知识结构图》

微分学核心公式

微分学核心公式

概率论知识结构

概率论知识结构

机器学习中的概率模型

机器学习中的概率模型

信息论知识结构

信息论知识结构

本文永久更新地址: https://notlate.cn/p/bae972c24d10482b/

最优化机器学习概率论与统计
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																				
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇 

                    

                    
			        推荐文章
		            

		            

							
计算广告-笔记10：基础知识储备