信息检索
倒排索引:从大量文档中查找包含某些词的文档集合
向量空间模型(Vector Space Model, VSM):最基础最重要的相似度度量方法之一
-
文档表示方法:用各个关键词在文档中的强度(如TF-IDF)组成的矢量来表示文档
-
词频(Term Frequency, TF):某文档中,该词出现的频率
-
倒数文档频率(Inverse document frequency, IDF):该词在所有文档中出现的频繁程度的倒数
- DF(m):出现词m的文档总数目
- N:总的文档数目
- 出现m的文档越多,则DF(m)越大,N不变,则IDF越小,表示该词重要性越低
-
相似度度量方法:一般采用余弦相似度
- 两个矢量在尺度上没有归一化时,仍然可以得到比较稳健的结果
最优化
给定某个确定的目标函数,及该函数自变量的一些约束条件,求解该函数的最大或最小值的问题
有约束的优化问题转化为无约束问题
-
拉格朗日乘子法
- 引入拉格朗日对偶函数,对偶问题的最优值是原问题最优值的下界
- 原问题是凸函数时,两者完全一致,称为强对偶。但是不是只有凸函数才是强对偶。
-
KKT条件
无约束问题求解方法
-
不可导或求导代价大
- 下降单纯形法
-
容易求导:线搜索方法
先确定方向,再计算步长- 梯度下降法
- 牛顿法
- 拟牛顿法
-
置信域法:每次迭代,将搜索范围限制到x的置信域内,然后同时决定下次迭代的方向和步长;如果当前置信域内找不到可行解,则缩小置信域范围。
统计机器学习
最大似然估计:
把模型的参数看成是固定的,找到使得训练数据上似然值最大的参数
-
最大熵(ME)
- 原理:当在某些约束条件下选择统计模型时,需要尽可能选择满足这些条件的模型中不确定性最大的那个。
- 最大熵解<==>对应指数型分布的最大似然解
-
指数族分布(单模态)
-
指数族分布参数的最大似然估计,可以完全由其充分统计量u(x)得到。
-
重要的指数族分布
- 高斯分布
- γ分布
- β分布
- 多项式分布
-
混合模型(多模态)
- 高斯混合模型(Mixture of Gaussians, MoG)
- 概率潜在语义索引(Probabilistic Latent Semantic Index, PLSI)
- EM算法
贝叶斯估计:
模型参数服从一定分布的随机变量
- 共轭先验
- 经验贝叶斯
深度学习
- 神经网络优化方法:梯度下降法
- 卷积神经网络CNN
- 循环神经网络RNN
- 生成对抗网络GAN
本文永久更新地址: https://notlate.cn/p/c4c4a6c224a9f5d2/
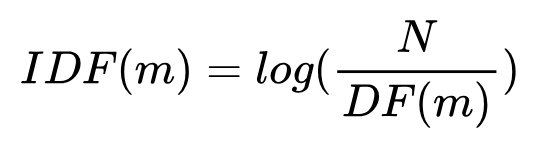
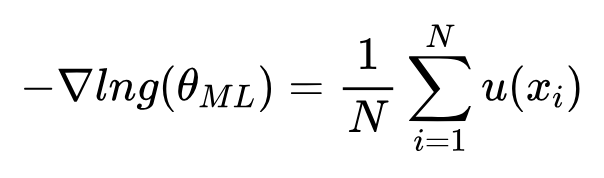
Thanks for sharing. I read many of your blog posts, cool, your blog is very good.
Your point of view caught my eye and was very interesting. Thanks. I have a question for you.
Your point of view caught my eye and was very interesting. Thanks. I have a question for you.
Can you be more specific about the content of your article? After reading it, I still have some doubts. Hope you can help me.
Your article helped me a lot, is there any more related content? Thanks!
Your point of view caught my eye and was very interesting. Thanks. I have a question for you.
Can you be more specific about the content of your article? After reading it, I still have some doubts. Hope you can help me.
Thanks for sharing. I read many of your blog posts, cool, your blog is very good.
Can you be more specific about the content of your article? After reading it, I still have some doubts. Hope you can help me.
Thanks for sharing. I read many of your blog posts, cool, your blog is very good.
Your article helped me a lot, is there any more related content? Thanks!